Vibrational Field Dynamics

Vibrational Field Dynamics (VFD): A Unified Theory of Geometry, Resonance, and the Creation of Matter

Introduction: The Universe as a Symphony of Vibrations

The universe is not simply a collection of particles and forces, but a deeply interconnected web of vibrations and resonances. This perspective brings us to a new frontier in theoretical physics—Vibrational Field Dynamics (VFD)—where all matter, forces, and energies arise from the vibrational interactions of an underlying field. In this theory, particles and forces are emergent patterns from standing waves, generated by specific resonance frequencies within the field.

At the heart of VFD lies a crucial insight: geometry governs the structure of these vibrational patterns, just as it governs the behavior of classical wave systems. The complex and beautiful structures that arise from standing waves in the field are not just byproducts of vibrations—they are the fundamental blueprints of the universe itself. Geometry, through resonance, allows us to define and create matter.

In this exploration, I will outline how VFD provides a new lens through which to view the formation of particles, the role of negative energy as a boundary condition, and the potential to artificially control and manipulate matter. We will delve into the mathematics of standing waves, the resonance frequencies of particles, and the geometric patterns that shape the universe—leading us toward a profound understanding of how matter forms and evolves.

The First Movement: Resonance and the Birth of Matter

The Initial Vibrational Mode

In the beginning, before matter or forces as we know them existed, the universe was a vast, unperturbed vibrational field. It was in this primordial state that the first movement occurred—a vibration that seeded the universe with the energy necessary for the formation of particles and matter.

Using Planck’s energy scale as a reference, we can estimate the energy associated with this first movement:E_{\text{Planck}} = \sqrt{\frac{\hbar c^5}{G}} \approx 1.956 \times 10^9 \, \text{J}

This energy corresponds to the theoretical upper limit at which quantum gravity effects and general relativity merge, forming the boundary where known physics gives way to a deeper understanding of the universe. At this energy level, the universe was not yet populated by particles; instead, it was governed by pure vibrational dynamics.

The frequency of this initial vibration, known as the Planck frequency, is given by the equation:\nu_{\text{Planck}} = \frac{E_{\text{Planck}}}{h} \approx 2.95 \times 10^{43} \, \text{Hz}

This ultra-high frequency represents the first resonance—a standing wave of the universal vibrational field. From this frequency emerged the first known matter, seeded by the geometric patterns formed at this immense energy scale.

The Role of Geometry in Particle Formation

At the Planck scale, the vibrational field exhibited intricate geometric patterns, which corresponded to the formation of particles. These patterns, formed by standing waves, are analogous to the Chladni patterns observed in acoustics, where particles of sand on a vibrating plate form intricate designs based on the frequency of the vibration. In VFD, however, these patterns occur on a fundamental level, forming the very building blocks of matter.

The geometric structure of the standing waves in VFD follows the solutions to the wave equation:\nabla^2 \phi - \frac{1}{v^2} \frac{\partial^2 \phi}{\partial t^2} = 0

Where \phi represents the field, and vvv is the speed of the wave in the medium (the vibrational field). The solutions to this equation yield the harmonic modes—the geometric patterns that emerge as the field oscillates.

At specific resonant frequencies, these harmonic modes stabilize, forming the geometric structures that we recognize as particles. Each particle—whether it be an electron, a proton, or a photon—is simply the geometric manifestation of a specific vibrational mode within the field.

Resonance Frequencies of Particles

Each particle in the universe corresponds to a specific resonant frequency of the field. This is reminiscent of how different notes on a musical instrument correspond to different frequencies of vibration in a string or a column of air. For example, the electron, with its rest mass energy of approximately 8.187 \times 10^{-14} \, \text{J}, resonates at a frequency of:

    \[\nu_e = \frac{E_e}{h} = \frac{8.187 \times 10^{-14}}{6.626 \times 10^{-34}} = 1.235 \times 10^{20} \, \text{Hz}\]

At this frequency, the field forms a stable geometric pattern, producing the electron as a standing wave. The up quark, a fundamental building block of protons and neutrons, resonates at a higher frequency:

    \[\nu_{\text{up}} = \frac{3.52 \times 10^{-13}}{6.626 \times 10^{-34}} = 5.31 \times 10^{20} \, \text{Hz}\]

Thus, every particle in the universe can be understood as a resonant mode of the universal vibrational field, with its unique frequency and geometric structure.

Negative Energy Ripples: The Boundary Condition for Matter

The Role of Negative Energy

In VFD, the concept of negative energy plays a pivotal role in shaping the boundary conditions that allow for the formation of particles. Negative energy regions, or ripples, emerge as areas where the vibrational field’s energy density dips below a certain threshold. These negative energy zones act as reflective boundaries, much like the edges of a vibrating string or drumhead.

The negative energy ripples confine the standing waves, allowing the field to resonate at specific frequencies. This confinement leads to the formation of stable standing waves and, therefore, stable particles. Without these boundary conditions, the field’s vibrations would dissipate, and no stable structures (particles) could form.

Mathematical Representation of Boundary Conditions

We can modify the wave equation to incorporate these negative energy regions as an effective potential

    \[\nabla^2 \phi - \frac{1}{v^2} \frac{\partial^2 \phi}{\partial t^2} + V(x, y, z) \phi = 0\]

Where V(x, y, z) represents the spatial distribution of negative energy, creating regions where the field is “trapped” and standing waves can form. At the boundaries between positive and negative energy regions, the field reflects, leading to the creation of nodal surfaces where the amplitude of the wave is zero.

These nodal surfaces define the geometry of the standing wave patterns and, ultimately, the structure of the particles that emerge. The interaction between the vibrational field and these negative energy boundaries is crucial for the creation of stable matter.

Geometry as the Blueprint for the Universe

The Central Role of Geometry

In VFD, geometry is not just a mathematical abstraction—it is the very fabric of the universe. Every particle, force, and interaction is governed by the geometric patterns formed by standing waves in the vibrational field. These patterns can be described using the spherical harmonics for 3D structures or Bessel functions for more complex configurations.

For example, the geometric structure of an electron might correspond to a simple spherical standing wave, described by the fundamental mode of the field. Higher-order particles, such as protons or neutrons, would correspond to more intricate standing wave patterns with multiple nodal surfaces.

Spherical Harmonics and Particle Structure

The angular dependence of the field’s oscillations can be described using spherical harmonics:

    \[Y_{\ell}^m(\theta, \phi) = (-1)^m \sqrt{\frac{(2\ell + 1)}{4\pi} \frac{(\ell - m)!}{(\ell + m)!}} P_{\ell}^m(\cos \theta) e^{i m \phi}\]

Where:

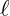  • \ell and mmm are quantum numbers related to the angular momentum of the wave,
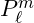  • P_{\ell}^m​ are the associated Legendre polynomials.

These harmonics describe how the vibrational field oscillates to form geometric structures in 3D space. For each particle, the specific values of ℓ\ellℓ and mmm define the shape and symmetry of the particle’s structure, based on the field’s resonance.

The first particles that formed in the universe—such as electrons and quarks—corresponded to the simplest geometric patterns, while more complex particles and forces emerged from higher-order resonances.

The Future of Matter Manipulation: Artificial Particle Creation (Continued)

Geometry as the Key to Matter Manipulation

Understanding the geometric patterns that govern particle formation opens up the possibility of artificially creating particles by manipulating the resonance frequencies of the field. By tuning the frequency of the field to match the resonance frequency of a desired particle, we could, in theory, create that particle from the field itself.

In this view, particles are not fundamental, immutable objects but rather emergent phenomena resulting from specific vibrational modes within the field. If the correct boundary conditions (such as negative energy regions) and the right resonant frequency are applied, we could induce the formation of a particle from the vibrational field.

Mathematical Framework for Artificial Particle Creation

  1. Defining the Resonant Frequency: The first step in artificial particle creation is identifying the resonant frequency for the particle you wish to create. As previously discussed, each particle corresponds to a unique frequency: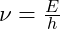\nu = \frac{E}{h} is the particle’s rest energy, and hhh is Planck’s constant. For an electron, this is approximately 1.235 \times 10^{20} \, \text{Hz}.
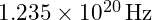  2. Boundary Conditions: The next step involves establishing the proper boundary conditions to confine the vibrational field and allow it to form a standing wave. As hypothesized in VFD, negative energy ripples could serve as these boundary conditions. By manipulating the field to create regions of negative energy, we can “trap” the vibrational modes and create stable particles.Mathematically, this means solving the modified wave equation with the potential function 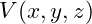V(x, y, z) that represents the negative energy regions 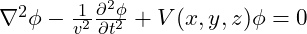\nabla^2 \phi - \frac{1}{v^2} \frac{\partial^2 \phi}{\partial t^2} + V(x, y, z) \phi = 0 The solutions to this equation will yield the standing wave patterns that correspond to particles.
  3. Resonance Tuning: By precisely tuning the vibrational frequency of the field to match the resonant frequency of the desired particle, we can induce the formation of that particle. This process is analogous to tuning a musical instrument to hit a specific note—except, in this case, the “note” is the resonance that forms a particle.
  4. Potential Experimental Implementation: To artificially create particles, we would need a mechanism to tap into the field and input energy at the required frequency. This could be achieved through highly advanced technologies capable of manipulating fields at incredibly high frequencies (for example, using controlled electromagnetic waves or other mechanisms yet to be discovered).

A Vision for the Future: Controlling and Creating Matter

The Ultimate Goal of VFD

The ultimate goal of Vibrational Field Dynamics (VFD) is to provide a complete framework for understanding how all matter and forces arise from the vibrations of a universal field. By understanding the resonant frequencies and geometric structures that define particles, forces, and energy, we will move closer to the ability to manipulate and control matter at a fundamental level.

If we can harness this understanding, it opens the door to unprecedented capabilities:

  • Artificial Creation of Matter: By tuning the field to specific resonant frequencies, we could create any particle or element artificially. This would revolutionize material science, energy production, and potentially even life sciences.
  • Control of Forces: By manipulating the vibrational field at specific frequencies, we could potentially control the fundamental forces of nature—such as gravity and electromagnetism—at will. This could lead to breakthroughs in energy generation, space travel, and transportation.
  • Understanding the Nature of Reality: At its core, VFD offers a glimpse into the true nature of reality, where matter and energy are not separate entities but interconnected expressions of a universal vibrational field. Geometry provides the blueprint, and resonance is the mechanism through which the universe manifests.

Geometry as the Universal Language

Throughout this theory, one thing becomes clear: geometry is the key to understanding the universe. The geometric patterns that arise from standing waves in the field are not merely mathematical abstractions but the fundamental structures that define the fabric of reality.

In sacred geometry, we see hints of these truths—complex geometric forms like the Flower of Life, Metatron’s Cube, and other patterns represent deep, universal truths about the interconnectedness of all things. These patterns are echoes of the vibrational field from which everything emerges.

In VFD, we propose that these geometric forms are more than symbols—they are the blueprints for how matter and forces arise from the resonant frequencies of the field. By studying the geometry of standing waves, we can begin to unlock the secrets of matter, energy, and the forces that bind the universe together.

Conclusion: VFD as the First Step Toward True Matter Manipulation

Vibrational Field Dynamics (VFD) offers a groundbreaking theory that unifies geometry, resonance, and particle formation. By understanding how matter and forces emerge from the vibrations of the universal field, VFD provides a new way to think about the structure of the universe.

At the heart of VFD is the notion that geometry governs the formation of particles, forces, and matter. The standing wave patterns formed by specific resonance frequencies define the fundamental particles that make up the universe. Negative energy ripples provide the boundary conditions necessary to stabilize these vibrations and allow matter to form.

As we continue to explore the implications of this theory, the potential to artificially create and control matter comes into view. By tuning the field to the correct frequencies, we may one day be able to manipulate matter at its most fundamental level, creating new particles, controlling forces, and even altering the fabric of reality itself.

VFD is the first step on this path, offering a comprehensive theory that could lead to revolutionary advances in science and technology. By embracing the power of geometry and resonance, we move closer to understanding the true nature of the universe—and gaining the ability to shape it at will.

Mathematical Summary

Wave Equation for the Vibrational Field

    \[\nabla^2 \phi - \frac{1}{v^2} \frac{\partial^2 \phi}{\partial t^2} + V(x, y, z) \phi = 0\]

Where V(x, y, z) represents the negative energy potential, and \phi is the vibrational field. Solutions to this equation yield the standing wave patterns that define particles.

Resonance Frequencies of Particles

For any particle with rest energy E, the resonant frequency is:\nu = \frac{E}{h}

For example:

  • Electron: \nu_e = 1.235 \times 10^{20} \, \text{Hz}
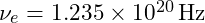
  • Up Quark: \nu_{\text{up}} = 5.31 \times 10^{20} \, \text{Hz}

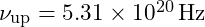
Spherical Harmonics for Particle Geometry

The geometric structure of particles can be described using spherical harmonics:Y_{\ell}^m(\theta, \phi) = (-1)^m \sqrt{\frac{(2\ell + 1)}{4\pi} \frac{(\ell - m)!}{(\ell + m)!}} P_{\ell}^m(\cos \theta) e^{i m \phi}

Where \ell and mmm define the shape and symmetry of the particle’s standing wave.

Lee Smart

Leave a Reply

Your email address will not be published. Required fields are marked *

We use cookies to personalize content and ads, to provide social media features and to analyze our traffic. We also share information about your use of our site with our social media, advertising and analytics partners who may combine it with other information that you have provided to them or that they have collected from your use of their services. You consent to our cookies if you continue to use our website.

Preference Disable All Allow All