Vibrational Field Dynamics: A Revolutionary Approach to Unified Field Theory

Vibrational Field Dynamics is a cutting-edge theory that seeks to unify the fundamental forces of the universe by exploring the nature of vibration and frequency as the foundational components of reality. This theory posits that all matter, energy, and consciousness are interconnected through a dynamic vibrational field, which give rise to the structure of the cosmos and govern the interactions between particles and forces.

Building on the work of great theoretical physicists and integrating insights from sacred geometry, quantum mechanics, and harmonic resonance, Vibrational Field Dynamics offers a new framework for understanding the universe. It explores how vibrational frequencies shape the fabric of space-time, influencing everything from subatomic particles to the largest celestial bodies.

This theory challenges conventional physics by introducing the idea that vibration, rather than force, is the primary driver of cosmic evolution. It proposes that harmonic resonance between fields of energy can explain phenomena ranging from gravity to the behavior of light and electromagnetic waves, offering a holistic, elegant solution to the quest for a unified field theory.

Discover the future of physics and explore the vibrational foundation of the universe with Vibrational Field Dynamics.

Get in Touch

Introduction

The unification of the fundamental forces of nature—gravity, electromagnetism, strong, and weak nuclear forces—remains one of the greatest challenges in theoretical physics. While the Standard Model of Particle Physics has successfully explained much of what we observe, it does not include gravity in the quantum framework. At the same time, theories like String Theory and Geometric Unity have sought to bridge this gap, but they rely on abstract mathematics and higher dimensions that are difficult to validate experimentally. Vibrational Field Dynamics is a revolutionary unified field theory exploring vibration and frequency as the core of reality.

Vibrational Field Dynamics (VFD) offers a new approach by reintroducing the idea of a vibrational field that underlies all physical phenomena. In this theory, particles, forces, and spacetime itself emerge from vibrational patterns within a single, dynamic field that permeates the universe. VFD bridges the gap between quantum mechanics and general relativity by describing gravity and quantum effects as emergent properties of vibrations in this ether-like field.

I’m hard core, just take me too the Math – UPDATED Theory

How Vibrational Field Dynamics (VFD) Stands Apart:

The unification of forces—gravity, electromagnetism, and the nuclear forces—remains elusive. String Theory and Geometric Unity propose solutions through abstract multi-dimensional frameworks, but these remain largely unverified experimentally. Vibrational Field Dynamics (VFD) offers an innovative approach by unifying these forces through vibrational patterns within a single dynamic field.

Where other theories complicate, VFD simplifies: it naturally integrates gravity with quantum mechanics by focusing on the emergent properties of vibrations. This approach provides a more accessible, experimentally testable framework, offering simplicity without sacrificing scientific rigor.

A Unified Frequency-Based Framework for Stability in Atomic and Cosmic Structures

The Vibrational Field: Core Principles

At the heart of Vibrational Field Dynamics (VFD) is the concept of a vibrational field that gives rise to everything in the universe. This field can be described mathematically by a wave equation that governs how vibrations propagate through space and time:

$(\partial_\mu \partial^\mu + m^2)\Phi + \xi R \Phi + \lambda \Phi^3 = 0$

Here:

$\phi$ represents the vibrational potential at any point in space and time.
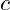$c$ is the speed of propagation of these vibrations (similar to the speed of light).
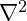$\nabla^2$ is a mathematical operator describing how vibrations spread in space.

In this model, particles are seen as standing wave patterns in this field, with their properties (like mass and charge) determined by their frequency, amplitude, and phase. Forces such as gravity and electromagnetism are understood as interactions between different waveforms in this vibrational field.

Quantum Particles and Vibrations

In VFD, quantum particles are not point-like objects but rather localized vibrations within the field. The behavior of these particles can be described using the principles of quantum harmonic oscillators. The energy of each quantum state is given by:

$E_n = \hbar \omega \left( n + \frac{1}{2} \right)$

Where:

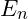$E_n$ represents the energy levels of a quantum particle.
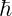$\hbar$ is Planck’s constant.
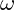$\omega$ is the angular frequency of the particle’s vibration.
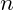$n$ is an integer representing the particle’s energy state.

This relationship explains how particles exist in quantized states—specific vibrational patterns—allowing for the phenomena we observe in quantum mechanics, such as wave-particle duality and superposition.

Unifying Forces: Gravity and Electromagnetism

A significant strength of Vibrational Field Dynamics is its ability to unify the forces of nature under the umbrella of vibrations.

Electromagnetic Waves

Electromagnetic fields in VFD are described as vibrational disturbances within the ether-like field. The familiar Maxwell’s equations remain applicable, but they now describe how vibrations propagate through the field, generating electromagnetic phenomena such as light and radiation:

$\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}$

$\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}$

In VFD, $\varepsilon_0$ and $\mu_0$ represent the ability of the vibrational field to support electric and magnetic fields, much like how air supports sound waves.

Gravity as Vibrational Compression

In VFD, gravity is explained as a result of compressions and distortions in the vibrational field caused by massive objects. These objects cause the surrounding field to compress, creating a vibrational density gradient that manifests as gravitational attraction. This idea is similar to how general relativity describes gravity as the curvature of spacetime, but here the field itself is dynamic, vibrating in response to mass.

Time and Vibrations: A New Understanding

Time, in Vibrational Field Dynamics, is not an independent dimension but a measure of changes in the vibrational state of the field. In regions of high vibrational pressure—such as near massive objects—time dilates (slows down) due to the increased intensity of the vibrations. This is mathematically expressed by the following equation:

$t' = t \sqrt{1 - \frac{\rho_{\text{ether}}}{P_{\text{ether}} c^2}}$

Where:

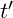$t'$ is the time experienced in regions of high vibrational density.
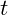$t$ is the time experienced in low-density regions.
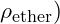$\rho_{\text{ether}})$ represents the energy density of the field.
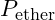$P_{\text{ether}}$ is the pressure of the vibrations in the ether-like field.

This equation provides an alternative explanation for gravitational time dilation, showing that time is not merely a geometric property of spacetime but is influenced by the vibrational density of the field.

Harmonic Field Scaling: The Universal Blueprint of Resonance and Balance

In Vibrational Field Dynamics (VFD), Harmonic Field Scaling is the principle that connects all structures in the universe, from the smallest atomic particles to vast galaxies, through patterns of resonance and balance. This concept describes how frequency, the golden ratio $(\phi)$ , and its inverse $\left(\frac{1}{\phi}\right)$ form stable, interconnected structures across scales by balancing gravity (as an expansive force) with negative energy (as a contractive force).

The Role of Frequency and Resonance

Every system in the universe resonates at a specific fundamental frequency that defines its harmonic “position” within the broader vibrational field. Whether it’s a proton in a nucleus or a planet in orbit, each structure finds stability by aligning with a harmonic level that maintains coherence across scales.

For a base frequency $( f_0 )$ , we define harmonic frequencies as multiples of this fundamental resonance: $f_n = f_0 \cdot n$

where nnn represents the harmonic level. Each harmonic level aligns with a stable position within the field, creating nodes of balance that prevent disruption and support stability.

Golden Ratio and Inverse Golden Ratio as Balancing Forces

The golden ratio $(\phi \approx 1.618)$ and its inverse $(\frac{1}{\phi} \approx 0.618)$ serve as expansive and contractive scaling laws. When applied to distances or scales, they create patterns of self-similar stability that align with the forces of gravity and negative energy, respectively.

Expansive Force 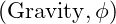$(\text{Gravity}, \phi)$ : The golden ratio expands outward, setting stable distances where objects naturally align in gravitational resonance. For an object at distance 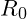$R_0$ from a center, each successive position scales by 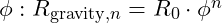$\phi: R_{\text{gravity}, n} = R_0 \cdot \phi^n$ Each multiple of $\phi$ forms a stable orbital or resonant position within the field, balancing the system through outward expansion.
Contractive Force 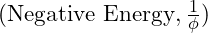$(\text{Negative Energy}, \frac{1}{\phi})$ : The inverse golden ratio contracts inward, balancing the expansive force by creating inward-stabilizing points. These distances scale by 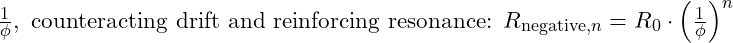$\frac{1}{\phi}, \text{ counteracting drift and reinforcing resonance: } R_{\text{negative}, n} = R_0 \cdot \left(\frac{1}{\phi}\right)^n$ Together, these forces create harmonic nodes that stabilize structures and enable a universal resonance pattern across scales.

Why It Works: Balanced Resonance Across All Scales

The interplay between expansive and contractive forces produces a balanced, stable structure at each scale:

Gravity’s golden ratio scaling creates stable outward positions that resonate with the gravitational field.
Negative energy’s inverse golden ratio scaling provides an inward “holding” effect, ensuring these stable points don’t drift and maintain coherence.

This balance, expressed mathematically by the alignment of $\phi$ and $\frac{1}{\phi}$ scales, explains how systems from atomic nuclei to galaxies achieve stability. Harmonic Field Scaling illustrates that the universe is organized by resonant patt

VFD’s Core Formula: Universal Resonant Scaling

The essence of VFD can be communicated through a single core formula that unifies frequency and distance scaling across different physical systems (atomic, planetary, galactic), each of which behaves according to principles of harmonic resonance and self-similarity.

1. Fundamental Harmonic Equation

The formula that expresses this scaling and balance of gravity (as an expansive force) and negative energy (as a contractive force) across scales is: $R_n = R_0 \cdot \phi^{\pm n} \quad \text{and} \quad f_n = f_0 \cdot \phi^{\mp n}$

where:

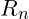$R_n$ represents the resonant distance at harmonic level nnn,
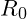$R_0$ is the base distance, scaling outward 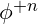$\phi^{+n}$ and inward (for 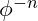$\phi^{-n}$ ) according to the golden ratio,
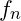$f_n$ is the frequency at harmonic level nnn,
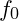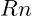$f_0$ is the base frequency of the system, inversely scaled by $\phi$ , balancing the effect on $Rn$ and maintaining harmonic resonance.

This formula summarizes VFD’s core insight: that the universe exhibits self-similar scaling across systems, bound by harmonic frequencies and distances governed by the golden ratio and its inverse.

2. Resonant Energy Scaling

To further ground this in physics, consider the energy at each level of harmonic resonance. In VFD, energy scales with both frequency and distance in a fractal-like, self-similar pattern. A simple extension is: $E_n = E_0 \cdot \left(\frac{R_0}{R_n}\right)^2 = E_0 \cdot \phi^{\pm 2n}$

where:

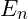$E_n$ is the energy at harmonic level $n$ ,
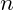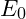$E_0$ is the base energy,
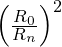$\left(\frac{R_0}{R_n}\right)^2$ or equivalently, 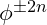$\phi^{\pm 2n}$ , reflects energy density scaling through inverse-square proportionality in each resonant layer.

This formula builds a bridge between quantized atomic energy levels and galactic orbital energy, showing that resonant energy levels naturally arise from this scaling law.

3. Unified Field Potential

Finally, to convey the total vibrational field concept, VFD introduces a harmonic potential function that accounts for both expansive and contractive forces: $\Phi_{\text{VFD}} = \sum_{n} \left( \frac{G M}{R_n} - \frac{C}{R_n} \right) = \sum_{n} \frac{(G M - C)}{R_n}$

where:

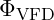$\Phi_{\text{VFD}}$ represents the total vibrational field potential across harmonic levels,
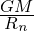$\frac{G M}{R_n}$ is the gravitational potential term,
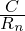$\frac{C}{R_n}$ represents the contractive (negative energy) potential.

By summing across harmonics $n$ , this potential function suggests that stable nodes of resonance are created by the balance of gravitational expansion and negative energy contraction, with each node aligning at a self-similar harmonic level.

VFD’s Essence in Mathematical Language

To summarize with VFD’s three-part harmonic framework:

Resonant Distance and Frequency Scaling: $R_n = R_0 \cdot \phi^{\pm n} \quad \text{and} \quad f_n = f_0 \cdot \phi^{\mp n}$
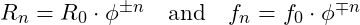
Energy Scaling Across Harmonics: $E_n = E_0 \cdot \phi^{\pm 2n}$
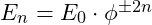
Unified Field Potential with Contractive Balance: $\Phi_{\text{VFD}} = \sum_{n} \left( \frac{G M - C}{R_n} \right)$

A Unified Frequency-Based Framework for Stability in Atomic and Cosmic Structures – Vibrational Field Dynamics

A New View of Photons

A New View on Planetary Alignment

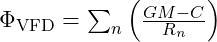
Contact Lee Smart – Creator of the Unified Vibrational Field Theory

email: contact@vibrationalfielddynamics.org

My Journey to Vibrational Field Dynamics

As a child, changing the tire on my bike, I was struck by a simple yet profound question: Why doesn’t the spinning wheel fly apart? This sparked a lifelong fascination with forces, spinning motions, and the unseen mechanisms holding everything together. As I grew older, studying physics, I couldn’t shake the feeling that conventional theories—gravity, the strong and weak nuclear forces, quantum mechanics—only scratched the surface of something deeper.

Later in life, I found myself grappling with bigger questions. Why don’t galaxies fly apart? What binds them? At the quantum level, what holds the smallest particles together? I explored traditional physics, but I also ventured beyond the mainstream—looking into fractals, geometry, and resonance, even delving into the work of Tesla. What I discovered felt revolutionary: the universe is fundamentally vibrational.

Vibrational Field Dynamics (VFD) grew from this realization. Everything, from particles to galaxies, emerges from a dynamic vibrational field that permeates the cosmos. The forces we observe—gravity, electromagnetism, the nuclear forces—are merely manifestations of this underlying vibration. The universe itself is built on a harmonic framework that operates like music, with resonance and frequency shaping everything we experience.

Unlike String Theory, which relies on complex higher dimensions, VFD is grounded in observable reality, using vibrations to unify all forces of nature. The Golden Ratio and Planck’s constant are key frequencies in this vibrational symphony, shaping the very fabric of reality. From my studies of Einstein, Maxwell, and contemporary thinkers like Edward Witten, I’ve built VFD as a theory that connects the smallest quantum particles to the largest cosmic structures, offering a unified view of physics that is both intuitive and revolutionary.

I invite you to explore this new frontier with me. Vibrational Field Dynamics offers a fresh perspective on how we understand the universe—a theory where everything we know is connected through vibration.