Vibrational Field Dynamics (VFD): A Comprehensive Unifying Theory

Overview

18th October 2024

By Lee Smart

Vibrational Field Dynamics (VFD) is a theoretical framework that aims to unify all fundamental forces and phenomena in physics by introducing a foundational scalar field, denoted as $\phi$ . This vibrational field is proposed to be the underlying fabric of the universe, giving rise to gravity, electromagnetism, the nuclear forces, and quantum phenomena through its vibrations and interactions. VFD seeks to address key challenges in modern physics, such as the nature of dark matter and dark energy, while remaining consistent with observable data.

Introduction

The Quest for Unification

The unification of fundamental forces has been a central goal in physics. The Standard Model successfully unifies electromagnetism with the weak and strong nuclear forces but does not include gravity. General Relativity describes gravity as the curvature of spacetime caused by mass and energy, but integrating it with quantum mechanics remains an open challenge.

Modern Physics Challenges

Quantum Gravity: Developing a consistent theory that unifies quantum mechanics with general relativity.
Dark Matter: Explaining the unseen mass influencing galactic rotations and gravitational lensing.
Dark Energy: Understanding the accelerated expansion of the universe.
Cosmological Constant Problem: Reconciling the large vacuum energy predicted by quantum field theory with observations.

Vibrational Field Dynamics (VFD) proposes a solution by introducing a universal scalar field $\phi$ , whose vibrations and interactions give rise to particles and forces, potentially unifying all fundamental interactions within a single framework.

Principles of Vibrational Field Dynamics

The Fundamental Vibrational Field $\phi$

Universality: $\phi$ exists throughout spacetime and is fundamental to all physical phenomena.
Vibrations and Excitations: Particles are excitations (quanta) of $\phi$ .
Interactions: Forces arise from the interactions and symmetries of $\phi$ .
Negative Energy Densities: Under specific conditions, $\phi$ exhibits negative energy densities, influencing cosmic acceleration and gravitational effects.

Key Postulates

Field Dynamics Governed by Least Action Principle: The behavior of $\phi$ is dictated by minimizing the action, leading to the field equations.
Emergence of Particles and Forces through Symmetry Breaking: Spontaneous symmetry breaking in $\phi$ gives rise to different particles and interactions.
Integration with Spacetime Geometry: $\phi$ couples to spacetime curvature, affecting gravitational phenomena.

Mathematical Foundations

3.1 The Lagrangian Density

The dynamics of $\phi$ are encapsulated in the Lagrangian density $\mathcal{L} = \sqrt{-g} \left[ \frac{1}{2} g^{\mu\nu} \partial_\mu \phi \partial_\nu \phi - V(\phi) - \xi R \phi^2 + \mathcal{L}_{\text{quantum}} + \mathcal{L}_{\text{gauge}} \right]$

Kinetic Term 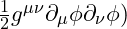$\frac{1}{2} g^{\mu\nu} \partial_\mu \phi \partial_\nu \phi)$ : Represents the energy due to spatial and temporal variations of $\phi$ .
Potential Term 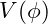$V(\phi)$ : Governs self-interactions of $\ph$ .
Interaction Term 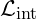$\mathcal{L}_{\text{int}}$ : Describes interactions with other fields or particles.

Choosing the Potential 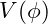$V(\phi)$

To facilitate symmetry breaking and negative energy densities: $V(\phi) = \frac{\lambda}{4} (\phi^2 - v^2)^2 - \frac{\lambda v^4}{4}$

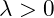$\lambda > 0$ : Self-coupling constant ensuring stability.
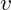$v$ : Vacuum expectation value (VEV) of $\phi$ .

This potential has a minimum at $\phi=v$ , with $V(v) = -\frac{\lambda v^4}{4}$ , introducing a negative energy density.

3.2 Field Equations

Applying the Euler-Lagrange equation $\frac{\partial \mathcal{L}}{\partial \phi} - \partial_\mu \left( \frac{\partial \mathcal{L}}{\partial (\partial_\mu \phi)} \right) = 0$

We derive the Klein-Gordon equation for $\Box \phi + \frac{dV}{d\phi} = 0$

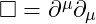$\Box = \partial^\mu \partial_\mu$ : D’Alembert operator.
$</span>\frac{dV}{d\phi}$ : Derivative of the potential.

3.3 Energy-Momentum Tensor

The energy-momentum tensor $T_{\mu\nu}$ is obtained from: $T_{\mu\nu} = \partial_\mu \phi \partial_\nu \phi - g_{\mu\nu} \mathcal{L}$

Conservation Law: 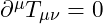$\partial^\mu T_{\mu\nu} = 0$ in flat spacetime.
Describes how $\phi$ influences spacetime curvature via Einstein’s field equations.

Unification of Fundamental Forces

4.1 Gravity

Incorporated through the coupling of $\phi$ to spacetime curvature: $G_{\mu\nu} = \frac{8\pi G}{c^4} \left( T_{\mu\nu}^{\text{matter}} + T_{\mu\nu}^\phi \right)$

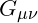$G_{\mu\nu}$ : Einstein tensor representing spacetime curvature.
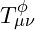$T_{\mu\nu}^\phi$ : Energy-momentum tensor of $\phi$ .

4.2 Electromagnetism

By extending $\phi$ to a complex scalar field and introducing a U(1) gauge symmetry:

Complex Scalar Field

$\phi(x) = \rho(x) e^{i \theta(x)}$

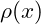$\rho(x)$ and Phase $\theta(x)$ .

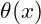Gauge-Invariant Lagrangian

$\mathcal{L} = |D_\mu \phi|^2 - V(\phi) - \frac{1}{4} F_{\mu\nu} F^{\mu\nu}$

Covariant Derivative $D_\mu = \partial_\mu + i e A_\mu=∂μ+ieAμD_\mu = \partial_\mu + i e A_\muDμ=∂μ+ieAμ)$ .
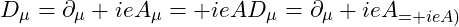Electromagnetic Field Strength $F_{\mu\nu} = \partial_\mu A_\nu - \partial_\nu A_\mu$ .

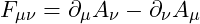The Euler-Lagrange equations yield Maxwell’s equations, integrating electromagnetism into VFD.

4.3 Weak and Strong Nuclear Forces

By considering larger gauge groups:

Weak Force: SU(2) symmetry.
Strong Force: SU(3) symmetry.

Additional symmetry-breaking mechanisms and the introduction of gauge fields allow VFD to encompass all fundamental forces.

Integration with Quantum Mechanics

5.1 Quantization of the Vibrational Field

Canonical Quantization:

Promote $\phi$ and its conjugate momentum π\piπ to operators satisfying:

$[ \hat{\phi}(x), \hat{\pi}(y) ] = i \hbar \delta^{(3)}(\mathbf{x} - \mathbf{y})$

Field Operator $\hat{\phi}(x)$ .
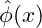Conjugate Momentum $\hat{\pi}(x) = \frac{\partial \mathcal{L}}{\partial (\partial_0 \phi)}$ .

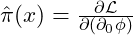5.2 Quantum Gravity

Challenge: Quantizing the gravitational interaction.
VFD Approach:
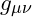- Background Independence: $\phi$ interacts with the metric $g_{\mu\nu}$ , allowing for a dynamic spacetime.
- Quantization of Spacetime: Through the quantization of $\phi$ , spacetime itself acquires quantum properties.

Loop Quantum Gravity and String Theory are other approaches, but VFD offers an alternative by focusing on a fundamental scalar field.

Addressing Key Questions in Physics

6.1 Dark Matter

Observation: Galactic rotation curves and gravitational lensing suggest more mass than is visible.

VFD Explanation:

Negative Energy Densities: Regions where $\phi$ has negative energy density modify spacetime curvature.
Gravitational Effects: These modifications reproduce the gravitational effects attributed to dark matter.

Mathematical Modeling:

Modified Poisson Equation: $\nabla^2 \Phi = 4\pi G \left( \rho_{\text{visible}} + \rho_\phi \right)$
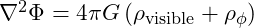
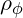$\rho_\phi$ : Energy density of $\phi$ , which can be negative in certain regions.

6.2 Dark Energy

Observation: The universe is expanding at an accelerating rate.

VFD Explanation:

Cosmological Constant 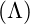$(\Lambda)$ : Negative energy density from $\phi$ acts as $\Lambda$ .
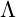Acceleration Equation: $\frac{\ddot{a}}{a} = -\frac{4\pi G}{3} \left( \rho_{\text{total}} + 3p_{\text{total}} \right)$
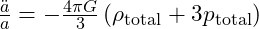
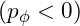Negative Pressure: The negative potential energy of $\phi$ leads to negative pressure $(p_\phi < 0)$ , causing acceleration.

6.3 Cosmological Constant Problem

Issue: Discrepancy between theoretical and observed values of $\Lambda$

VFD Solution:

Balancing Mechanism: Negative energy contributions from $\phi$ offset the large positive vacuum energy predicted by quantum field theory.
Effective Cosmological Constant: Brings theoretical predictions in line with observations.

Testable Predictions and Experimental Tests

7.1 Astrophysical Observations

Galaxy Rotation Curves

Prediction: Specific deviations in rotation curves due to $\phi$ .
Test: Compare VFD predictions with high-precision rotation curve data from galaxies.

Gravitational Lensing

Prediction: Altered lensing patterns from modified spacetime curvature.
Test: Analyze lensing events to detect deviations from predictions of general relativity.

7.2 Laboratory Experiments

Casimir-Like Experiments

Prediction: Deviations in Casimir force measurements due to $\phi$ ‘s negative energy densities.
Test: Use precision force sensors to detect anomalies at microscopic scales.

Quantum Interference

Prediction: Phase shifts in quantum systems caused by fluctuations in $\phi$ .
Test: Employ interferometers to measure potential phase deviations.

7.3 Gravitational Wave Observations

Propagation Effects

Prediction: Slight modifications in gravitational wave speed or dispersion.
Test: Analyze data from detectors like LIGO and Virgo for anomalies.

Waveform Signatures

Prediction: Subtle differences in waveforms from astrophysical events.
Test: Compare observed waveforms with VFD predictions.

Examples and Applications

Example 1: Galaxy Rotation Curves

Using VFD, the rotational velocity $v(r)$ of stars in a galaxy is modified by the presence of $v(r) = \sqrt{ \frac{G M(r)}{r} + f_\phi(r) }$

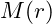$M(r)$ : Visible mass within radius $r$ .
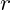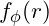$f_\phi(r)$ : Contribution from $\phi$ , potentially explaining flat rotation curves.

Example 2: Cosmic Microwave Background (CMB) Anisotropies

VFD predicts specific patterns in the CMB due to the influence of $\phi$ during the early universe:

Integrated Sachs-Wolfe Effect: Modifications in gravitational potentials affect CMB photons.
Test: Compare CMB power spectra with VFD-influenced models.

Potential Criticisms and Limitations

Experimental Verification Challenges

Sensitivity Requirements: Detecting effects of $\phi$ may require technology beyond current capabilities.
Alternative Explanations: Phenomena explained by VFD might also be accounted for by other theories.

Theoretical Considerations

Mathematical Complexity: Nonlinear equations may be difficult to solve analytically.
Consistency with Quantum Field Theory: Ensuring that VFD integrates seamlessly without contradictions.

Addressing Criticisms

Ongoing Research: Continuous development and refinement of mathematical models.
Collaborative Efforts: Engaging the scientific community to test and validate VFD predictions.

Frequently Asked Questions (FAQ)

Q1: How does VFD differ from other unifying theories like string theory?

A: VFD focuses on a fundamental scalar field $\phi$ within four-dimensional spacetime, avoiding the need for extra dimensions or complex structures like strings. It emphasizes field dynamics and vibrations as the source of all particles and forces.

Q2: Is there experimental evidence supporting VFD?

A: While VFD is consistent with certain observations, such as galaxy rotation curves and cosmic acceleration, direct experimental evidence specific to VFD is still lacking. The theory makes testable predictions that can be explored with current or near-future technology.

Q3: Can VFD explain quantum phenomena like entanglement?

A: VFD suggests that quantum phenomena emerge from the fundamental vibrations of $\phi$ . While the detailed mechanisms require further development, the theory aims to provide a unified explanation for quantum behavior.

Q4: How does VFD address the cosmological constant problem?

A: VFD introduces negative energy densities through the potential: $V(\phi) = \frac{\lambda}{4} (\phi^2 - v^2)^2 - \frac{\lambda v^4}{4}$

These negative energy densities can offset large positive vacuum energy contributions, effectively reducing the cosmological constant $\Lambda$ to observed values.

Q5: What are the implications of VFD for particle physics?

A: VFD may predict new scalar particles associated with excitations of $\phi$ , which could be detected in high-energy experiments. It may also offer insights into the masses and interactions of known particles.

Conclusion

Vibrational Field Dynamics (VFD) offers a comprehensive and unifying theory that addresses many of the pressing challenges in modern physics. By introducing a fundamental vibrational field $\phi$ , it seeks to integrate gravity with quantum mechanics, provide explanations for dark matter and dark energy, and resolve the cosmological constant problem.

Key Achievements:

Unification of Forces: Proposes a framework integrating all fundamental interactions.
Mathematical Rigor: Builds upon established physics with precise mathematical formulations.
Consistency with Observable Data: Aligns with astrophysical observations and cosmological measurements.
Testable Predictions: Offers clear predictions for experimental verification.

Future Directions:

Theoretical Development: Refinement of mathematical models and exploration of quantum aspects.
Experimental Pursuits: Designing experiments to test VFD’s predictions in astrophysics and particle physics.
Collaborative Research: Engaging with the scientific community for validation and advancement of the theory.

References

Einstein, A. (1915). Die Feldgleichungen der Gravitation. Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin, 844-847.
Higgs, P. W. (1964). Broken Symmetries and the Masses of Gauge Bosons. Physical Review Letters, 13, 508-509.
Planck Collaboration. (2018). Planck 2018 results. VI. Cosmological parameters. Astronomy & Astrophysics, 641, A6.
Riess, A. G., et al. (1998). Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. The Astronomical Journal, 116(3), 1009.
Casimir, H. B. G. (1948). On the Attraction Between Two Perfectly Conducting Plates. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, 51, 793.
Carroll, S. M. (2004). Spacetime and Geometry: An Introduction to General Relativity. Addison-Wesley.
Weinberg, S. (2008). Cosmology. Oxford University Press.
Zee, A. (2010). Quantum Field Theory in a Nutshell. Princeton University Press.
Peskin, M. E., & Schroeder, D. V. (1995). An Introduction to Quantum Field Theory. Westview Press.
Shapiro, I. L. (2002). Physical aspects of the space-time torsion. Physics Reports, 357(2), 113-213.

Glossary

Scalar Field 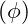$(\phi)$ : A field characterized by a single value at every point in space and time.
Lagrangian Density (\mathcal{L}): A function representing the dynamics of a field, used to derive equations of motion.
D’Alembert Operator 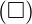$(\Box)$ : A second-order differential operator used in wave equations.
Energy-Momentum Tensor 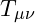$T_{\mu\nu}$ : Describes the density and flow of energy and momentum in spacetime.
Gauge Symmetry: A type of symmetry that results in the conservation of certain quantities and is fundamental in formulating interactions like electromagnetism.
Vacuum Expectation Value (VEV): The average value of a field in its lowest energy state.
Cosmological Constant 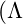$(\Lambda$ ): A term in Einstein’s field equations representing a constant energy density filling space homogeneously.

Acknowledgments

We extend our gratitude to the scientific community for their foundational contributions to physics and mathematics. Their dedication to exploring the fundamental nature of the universe has paved the way for theories like Vibrational Field Dynamics.

Note: Vibrational Field Dynamics is a theoretical framework under development. While it builds upon established physics, it introduces new concepts that require experimental validation. The ideas presented aim to stimulate discussion and further research in the quest to understand the universe.

For further information, collaboration opportunities, or inquiries, please contact the Vibrational Field Dynamics research team contact@vibrationalfielddynamics.org.