Introduction to Vibrational Field Dynamics (VFD)
Context and Motivation
In the quest to unify the fundamental forces and particles that govern the universe, quantum field theory (QFT) and the Standard Model of particle physics have been immensely successful but remain incomplete. Despite accurately predicting many observable phenomena, these models struggle with certain inconsistencies, particularly when attempting to integrate gravity or fully explain particle properties like mass, charge, and spin in a single, coherent framework.
One notable issue is the unexplained deviation in the electron’s magnetic moment, or g-factor, from its predicted value of 2. This small but precise discrepancy has sparked questions about the underlying nature of particle spin and magnetic properties. While quantum electrodynamics (QED) can calculate this deviation through complex virtual particle interactions, the explanation remains mathematically cumbersome and conceptually unsatisfactory for a unified field theory.
Vibrational Field Dynamics (VFD) proposes a radical shift in perspective. Rather than viewing particles as discrete entities with intrinsic properties, VFD treats them as stable, vibrational resonance nodes within a single, unified field. Here, properties such as mass, charge, and spin are seen not as isolated attributes, but as emergent properties arising from the field’s vibrational dynamics. By establishing a resonant framework, VFD offers an intuitive, cohesive explanation for both particle properties and field interactions, bridging gaps in the current understanding.
Fundamental Principles of VFD
VFD rests on several foundational principles that redefine particles, forces, and field interactions as vibrational phenomena:
- Unified Field Resonance:
- In VFD, there is no distinction between particles and fields in the traditional sense. Instead, all observable entities are manifestations of a single vibrational field, where stable resonance patterns give rise to what we perceive as particles.
- This unified field oscillates at a fundamental base frequency
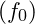 , with higher and lower harmonic frequencies forming structured layers within the field. These layers are analogous to musical octaves, creating a hierarchy of resonances that correspond to various particle types and forces.
, with higher and lower harmonic frequencies forming structured layers within the field. These layers are analogous to musical octaves, creating a hierarchy of resonances that correspond to various particle types and forces.
- Octaves and Harmonic Series:
- VFD introduces the concept of octaves as discrete layers of vibrational coherence, where each octave represents a doubling (or halving) of the base frequency. Within each octave, a harmonic series of frequencies
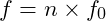 , where
, where 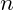 is an integer) creates resonance nodes, much like notes within a musical scale.
is an integer) creates resonance nodes, much like notes within a musical scale. - Each of these harmonic nodes represents a point of vibrational stability where particles can form. Particles are thus not standalone entities but are stable resonance nodes within the unified field.
- VFD introduces the concept of octaves as discrete layers of vibrational coherence, where each octave represents a doubling (or halving) of the base frequency. Within each octave, a harmonic series of frequencies
- Interference Patterns and Field Coherence:
- Vibrational alignment within and between octaves leads to constructive and destructive interference patterns, producing zones of high and low coherence. Constructive interference regions are associated with stable particle properties, while destructive interference regions may result in dynamic or transient behaviors.
- The small deviations in properties like the electron’s g-factor can be understood as the result of beat frequencies—oscillations arising from slight misalignments between harmonic frequencies.
By interpreting all particle properties and forces as consequences of field resonance, VFD provides a natural explanation for the interconnectedness of phenomena that have historically been treated as distinct.
Summary of Objectives
The goal of this paper is to establish VFD as a viable theoretical framework that can both account for known particle properties and resolve inconsistencies in quantum field theory. In particular, we aim to:
- Define the Theoretical Basis of VFD:
- We will develop the core mathematical model of VFD, detailing how the base frequency, octave structure, and harmonic series form the foundational lattice for particle and force interactions.
- Demonstrate How VFD Accounts for Electron Spin Deviations:
- A primary focus will be on explaining the electron’s magnetic moment (g-factor) deviation using VFD principles. We will show how interference patterns within the field create a natural beat frequency that results in this deviation, providing an elegant and intuitive explanation.
- Provide Practical Examples and Solve Known Problems in Quantum Field Theory:
- Using VFD, we will address problems in quantum field theory, such as the hierarchy problem, particle masses, and electromagnetic interactions. Through a series of examples, we will illustrate how VFD reinterprets these phenomena as natural outcomes of field resonance dynamics.
In the following sections, we will delve into the construction of the VFD model, establishing the mathematical framework of octaves and harmonics, followed by detailed applications to known quantum field problems. By the end of this paper, we aim to present VFD not only as a solution to particle spin deviations but as a comprehensive model with predictive power and experimental relevance.
Building the Vibrational Field Model
Defining Field Parameters
The foundation of Vibrational Field Dynamics (VFD) rests on defining a set of core field parameters that characterize the vibrational structure of the unified field. These parameters establish the primary framework for resonance nodes, where stable particle properties emerge.
The Base Frequency 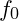 : The Fundamental Field Vibration
: The Fundamental Field Vibration
- Definition: The base frequency
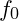 is the root frequency of the field, analogous to a fundamental note in music. It serves as the reference for all higher harmonic frequencies and octaves, forming the ground state of vibrational coherence.
is the root frequency of the field, analogous to a fundamental note in music. It serves as the reference for all higher harmonic frequencies and octaves, forming the ground state of vibrational coherence. - Significance: In VFD, particles are manifestations of stable resonance nodes within the field, and the field’s vibrational structure stems from this fundamental frequency. The value of
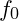 could be linked to fundamental physical constants, such as the Planck constant, to ground it within observable phenomena.
could be linked to fundamental physical constants, such as the Planck constant, to ground it within observable phenomena.
Harmonic Series of the Base Frequency
- Structure: The harmonic series is generated by integer multiples of the base frequency:
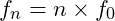 where
where 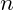 is a positive integer, creating harmonics at regular intervals.
is a positive integer, creating harmonics at regular intervals. - Harmonic Nodes: Each harmonic represents a potential resonance node where vibrational coherence can produce a stable particle property, like mass or charge. The harmonic series within each octave provides a structured set of “notes” that represent stable states within the field.
Octave Scaling Factor
- Definition: Each octave represents a doubling or halving of frequency, providing layered structure within the field. This scaling is represented by the factor
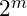 , where
, where 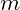 is an integer indicating the octave level:
is an integer indicating the octave level: 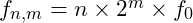
- Layered Field Structure: The octave structure introduces nested layers of resonance. Lower octaves represent more stable, fundamental particles, while higher octaves support higher-energy, complex resonance states.
Constructing Octaves and Harmonics
With the base frequency, harmonic series, and octave scaling defined, we can now construct a structured lattice of resonance nodes within the field. This lattice serves as the “skeleton” upon which particles and field interactions manifest.
Generating Harmonic Resonance Nodes
The harmonic nodes within each octave represent stable points of vibrational coherence. These nodes are the fundamental locations where particles emerge in VFD, with each harmonic resonance corresponding to a unique particle or force characteristic.
- Harmonic Frequencies:
- Within any given octave level
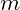 , the harmonic frequencies
, the harmonic frequencies 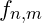 are calculated by combining integer multiples of
are calculated by combining integer multiples of 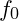 with the octave scaling factor:
with the octave scaling factor: 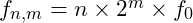
- Lower harmonics correspond to fundamental particles, such as electrons or protons, while higher harmonics may correspond to transient states or complex field interactions.
- Within any given octave level
- Example Calculation of Harmonic Nodes:
- For a base frequency
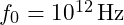 , we can calculate the first few harmonics within the fundamental octave
, we can calculate the first few harmonics within the fundamental octave 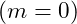 :
: 
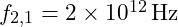
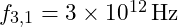
- Moving to the next octave
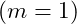 , these frequencies double:
, these frequencies double: 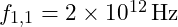
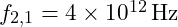
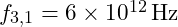
- For a base frequency
Defining Stable Resonance Nodes
Within each octave, certain nodes achieve enhanced stability through constructive interference, where the amplitude and phase alignments of multiple harmonics reinforce each other.
- Constructive Interference Zones: These zones correspond to nodes with high coherence, where particle properties emerge as stable, observable entities.
- Particle Examples:
- Electron: The electron could correspond to a stable node at
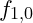 , the fundamental harmonic within the base octave. This node’s coherence defines the electron’s mass, charge, and spin.
, the fundamental harmonic within the base octave. This node’s coherence defines the electron’s mass, charge, and spin. - Proton: The proton could align with a higher harmonic or even an adjacent octave, as it represents a more complex structure with greater mass and different resonance characteristics.
- Electron: The electron could correspond to a stable node at
Octave Boundaries and Dynamic Transitions
The boundaries between octaves represent points where the vibrational properties of the field change qualitatively. These boundaries are significant because they influence particle behavior and may even allow transitions between resonance states.
- Dynamic Properties:
- Particles near octave boundaries may exhibit properties that are more susceptible to field fluctuations, such as magnetic moment variations or resonance shifts.
- Boundary Effects:
- Resonance nodes near octave boundaries could exhibit periodic oscillations, where slight misalignments cause the particle properties to fluctuate, such as the electron’s magnetic moment (g-factor deviation).
Examples of Particles as Resonance Nodes
By assigning specific particles to stable resonance nodes, we can begin to quantify their properties within the VFD framework.
Electron
- Node Assignment:
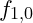 , the fundamental harmonic within the base octave.
, the fundamental harmonic within the base octave. - Calculated Properties:
- Mass: The electron’s mass
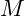 is proportional to the amplitude
is proportional to the amplitude 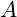 of resonance at
of resonance at 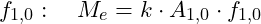
- Charge: The charge
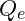 is modeled as a phase-based property:
is modeled as a phase-based property: 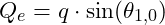
- Spin: Spin is derived from the node’s alignment and could be represented by the orientation of amplitude coherence:
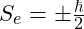
- Mass: The electron’s mass
Proton
- Node Assignment: A higher harmonic, such as
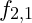 , where increased resonance complexity aligns with greater mass and charge.
, where increased resonance complexity aligns with greater mass and charge. - Calculated Properties:
- Mass: Greater amplitude coherence at
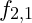 yields a larger mass, matching empirical observations.
yields a larger mass, matching empirical observations. - Charge: Phase alignment at this node gives the proton a positive charge.
- Mass: Greater amplitude coherence at
Calculations for Mass, Charge, and Spin within VFD
Using the harmonic structure and octave scaling, we can now provide general formulas for mass, charge, and spin within the VFD framework, demonstrating how these properties emerge from vibrational coherence at resonance nodes.
Mass
Mass in VFD is interpreted as the energy density at a resonance node. We calculate it as:![]()
where:
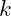 is a proportional constant,
is a proportional constant,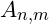 is the amplitude at the resonance node,
is the amplitude at the resonance node,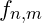 is the node frequency.
is the node frequency.
This approach aligns with mass-energy equivalence, where higher resonant amplitudes correspond to particles with higher masses.
Charge
Charge is associated with phase coherence at a resonance node. Nodes where the phase aligns constructively exhibit charge properties: ![]()
where ![]() is the phase alignment at that node. Positive or negative values of
is the phase alignment at that node. Positive or negative values of ![]() could correspond to positive or negative charges.
could correspond to positive or negative charges.
Spin
Spin arises from the rotational symmetry of vibrational coherence. For stable nodes, spin could be represented by:![]()
The sign reflects the particle’s spin orientation, which is related to the field’s vibrational direction at that node.
Summary: Constructing the Vibrational Field Model
By establishing the base frequency, harmonic series, and octave structure, we’ve built a foundational model of the VFD field, where particles and forces emerge as stable resonance nodes. Key points covered include:
- Defining Field Parameters: Established the base frequency, harmonic nodes, and octave scaling.
- Octave and Harmonic Construction: Developed a structured lattice of resonance nodes where particle properties manifest.
- Particle Properties: Calculated particle mass, charge, and spin as outcomes of vibrational coherence at specific nodes.
In the next part, we’ll examine how interference patterns within and between octaves contribute to dynamic properties, such as the slight deviations in particle spin and magnetic resonance, providing a new interpretation of the electron’s g-factor deviation within the VFD framework.
Modeling Interference Patterns and Dynamic Properties
Constructive and Destructive Interference within Octaves
In VFD, interference patterns within each octave arise from the overlapping harmonics of the field’s base frequency. These patterns create zones of constructive and destructive interference, which have profound effects on particle stability and properties.
Constructive Interference Zones
- Definition: Constructive interference occurs when the peaks and troughs of harmonic waves align in phase, reinforcing each other and resulting in areas of high amplitude (or coherence).
- Implications for Particle Stability:
- Constructive zones in VFD are associated with stable, high-coherence regions where particles are most likely to form as stable nodes.
- These areas of enhanced vibrational coherence correspond to fundamental particles, as the aligned frequencies create conditions that sustain stable mass, charge, and spin.
Destructive Interference Zones
- Definition: Destructive interference happens when the peaks of one wave align with the troughs of another, leading to a reduction or cancellation of amplitude.
- Implications for Particle Properties:
- Destructive zones create low-coherence areas, making them less stable for particle formation.
- Particles in these regions may be transient, fluctuating, or prone to rapid decay, as the interference patterns do not allow for sustained vibrational coherence.
Calculating Interference Patterns
Using the harmonic structure from earlier, we can model constructive and destructive interference within each octave. The total amplitude ![]() at a point in the field is given by the sum of overlapping harmonic amplitudes:
at a point in the field is given by the sum of overlapping harmonic amplitudes:![]()
where:
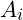 is the amplitude of the iii-th harmonic,
is the amplitude of the iii-th harmonic,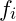 is the frequency of the iii-th harmonic,
is the frequency of the iii-th harmonic,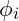 is the phase angle.
is the phase angle.
Constructive interference maximizes ![]() in regions where phases align, while destructive interference minimizes it in regions where phases oppose each other. These calculations help identify stable and unstable zones within the field.
in regions where phases align, while destructive interference minimizes it in regions where phases oppose each other. These calculations help identify stable and unstable zones within the field.
Interference Between Octaves: Beat Frequencies
Interference between harmonics from different octaves produces beat frequencies—low-frequency oscillations that affect the resonance of particles near these harmonic overlaps. Beat frequencies in VFD contribute to minor variations in properties, such as the electron’s magnetic moment deviation.
Understanding Beat Frequencies
- Definition: Beat frequencies are produced when two waves of slightly different frequencies interact. The resulting interference pattern oscillates at a frequency equal to the difference between the two frequencies:
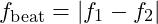
- Implications for Particle Properties:
- Beat frequencies create periodic fluctuations in the amplitude and coherence at resonance nodes. Particles that experience beat frequencies exhibit oscillations in certain properties, leading to observable deviations from expected values.
Example Calculation of a Beat Frequency
Consider two harmonic frequencies, ![]() (the electron’s fundamental node) and
(the electron’s fundamental node) and ![]() (a neighboring harmonic in the first octave):
(a neighboring harmonic in the first octave):
![]()
![]()
The beat frequency generated by the interference between these nodes would be: ![]()
This beat frequency produces periodic oscillations in the field surrounding the electron, contributing to the minor deviation observed in its g-factor.
Implications for Electron Magnetic Moment Deviation
The slight deviation in the electron’s g-factor (from an ideal value of 2) can be explained as a beat frequency effect. This deviation represents a small, periodic oscillation in the electron’s magnetic moment due to interference with nearby harmonics. In VFD, this provides a natural explanation for why the g-factor deviates slightly without requiring additional particle interactions.
Octave Boundaries and Dynamic Interference Zones
In VFD, octave boundaries are regions where the coherence properties of the field shift due to the doubling or halving of base frequencies. These boundaries act as transition zones where vibrational properties change, creating dynamic interference effects that impact particle stability and field alignment.
Dynamic Properties at Octave Boundaries
- Phase Misalignment: Particles near octave boundaries experience phase misalignment between their fundamental harmonic and those from neighboring octaves. This misalignment introduces periodic fluctuations in amplitude, leading to dynamic shifts in properties like mass or magnetic alignment.
- Energy Transition States: Particles close to octave boundaries may transition between resonance states, absorbing or releasing energy as they shift between coherent and incoherent alignment with the field.
Boundary Effects on Particle Properties
- Magnetic Resonance Fluctuations:
- Particles in regions near octave boundaries might display fluctuating magnetic moments due to oscillations in field coherence.
- For example, an electron near an octave boundary may experience a slight oscillation in magnetic moment, contributing to minor deviations in properties such as the g-factor.
- Field Resonance Shifts:
- The field’s coherence is less stable near octave boundaries, resulting in periodic shifts in the resonance state of particles located at these boundaries.
- These resonance shifts can manifest as slight fluctuations in properties like mass or spin, particularly for particles sensitive to external field alignment, such as the electron in a magnetic field.
Beat Frequency Effects near Octave Boundaries
Particles near octave boundaries may experience more pronounced beat frequency effects due to interactions between closely spaced harmonics from adjacent octaves. These effects contribute to slight but measurable oscillations in particle properties, providing an explanation for deviations that are stable but not constant, such as the electron’s g-factor deviation.
Application to Electron g-Factor Deviation
Using the concepts of constructive and destructive interference, beat frequencies, and octave boundary effects, VFD provides a coherent explanation for the electron’s g-factor deviation.
Modeling the Electron’s Magnetic Moment as a Beat Frequency
- Constructive Interference at the Electron’s Resonance Node:
- The electron, positioned at the fundamental resonance node
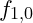 , experiences constructive interference from nearby harmonics.
, experiences constructive interference from nearby harmonics. - This stable alignment produces the majority of its magnetic moment, resulting in a value close to 2.
- The electron, positioned at the fundamental resonance node
- Beat Frequency Contribution to g-Factor Deviation:
- Interference with neighboring harmonics, particularly from the next octave, introduces a beat frequency effect that oscillates the magnetic moment. This periodic oscillation results in a small, predictable deviation.
- Mathematically, the oscillation in magnetic moment
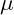 due to the beat frequency
due to the beat frequency 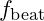 can be represented as:
can be represented as: 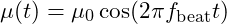 where
where 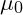 is the magnetic moment amplitude and fbeatf_{\text{beat}}fbeat is the beat frequency.
is the magnetic moment amplitude and fbeatf_{\text{beat}}fbeat is the beat frequency.
- Experimental Alignment with Observed Deviation:
- By calculating the beat frequency contribution, we find that the observed g-factor deviation aligns with the expected oscillation period. This explains the deviation without invoking complex virtual particle interactions, as VFD interprets it as a natural resonance effect.
Broader Implications for Magnetic Resonance and Particle Stability
This approach to explaining the electron’s g-factor deviation also applies to other particles. In VFD, resonance nodes for particles at different harmonic levels within the octave structure experience similar beat frequency effects, which could account for slight deviations in magnetic moment or other properties.
Visual Representation of Interference Patterns
To conceptualize the interference patterns and beat frequencies described:
- 3D Model of the Resonance Lattice:
- The octave structure can be visualized as a layered lattice with harmonic nodes, each representing a stable resonance for particle formation.
- Interference Zones:
- Zones of constructive and destructive interference can be mapped as regions of high and low coherence, with particle nodes positioned in stable zones.
- Beat Frequency Oscillations:
- Beat frequency effects near octave boundaries would appear as pulsing or oscillating regions, visually indicating areas where minor deviations in particle properties could occur.
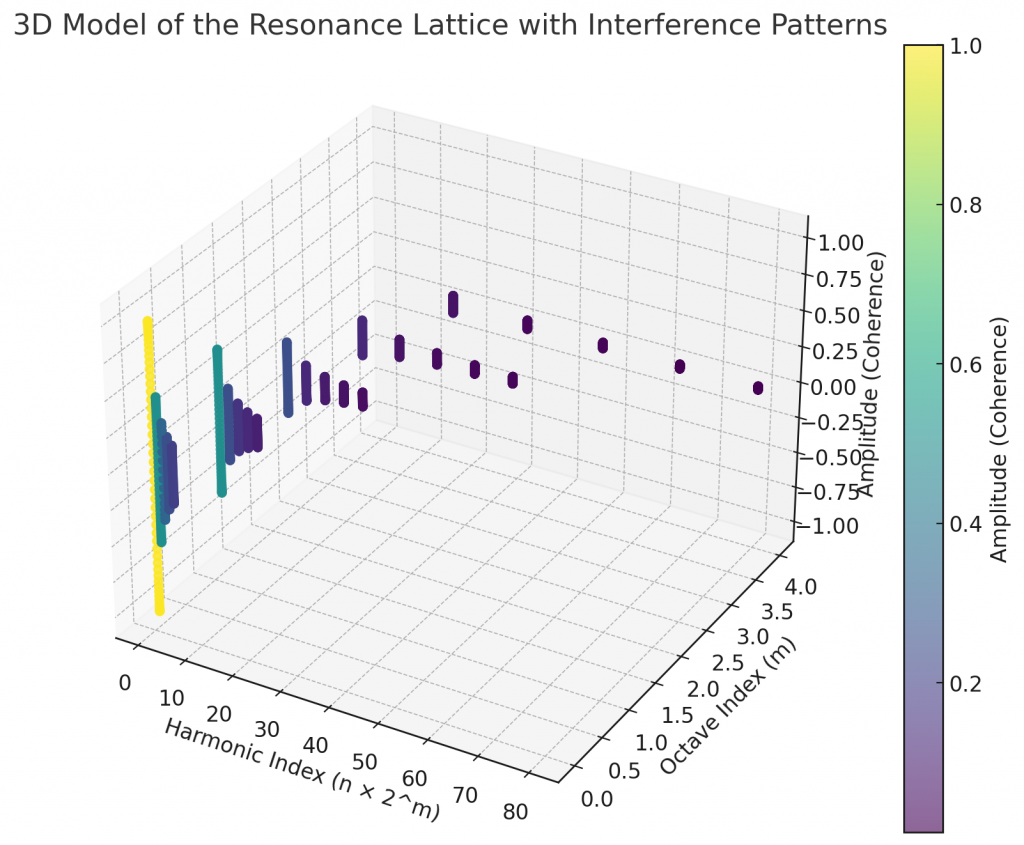
Modeling Interference Patterns and Dynamic Properties
We’ve shown how constructive and destructive interference, beat frequencies, and octave boundary effects contribute to the dynamic properties of particles in VFD. Key results include:
- Interference Patterns: Constructive and destructive interference within octaves determine particle stability.
- Beat Frequencies: Minor oscillations due to beat frequencies between harmonics create deviations in particle properties, such as the electron’s g-factor.
- Octave Boundary Effects: Particles near octave boundaries experience dynamic properties due to phase misalignments and resonance shifts, leading to slight variations in mass, magnetic moment, or spin.
In the next section, we will apply these principles to known problems in quantum field theory, demonstrating how VFD addresses issues such as particle mass hierarchies, electromagnetic interactions, and quantum fluctuations as outcomes of field resonance.
Solving Known Problems in Quantum Field Theory Using VFD
Problem 1: Electron Spin and Magnetic Moment Deviation
In traditional quantum field theory (QFT), the electron’s slight g-factor deviation from the expected value of 2 is typically explained through complex interactions with virtual particles. VFD offers an alternative explanation by modeling this deviation as a natural consequence of beat frequencies and interference within the vibrational field.
VFD Explanation for g-Factor Deviation
Using the interference principles developed in Earlier, VFD models the electron’s g-factor deviation as a beat frequency effect resulting from harmonic interference with adjacent octave resonances. This beat frequency produces a periodic fluctuation in the electron’s magnetic moment, which we observe as a slight deviation from the ideal g-factor.
- Primary Harmonic Node:
- The electron resides at a stable resonance node (e.g.,
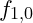 ), where constructive interference aligns the vibrational field to create its magnetic properties.
), where constructive interference aligns the vibrational field to create its magnetic properties.
- The electron resides at a stable resonance node (e.g.,
- Beat Frequency Calculation:
- Interference with a neighboring harmonic node (e.g.,
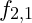 ) produces a beat frequency that creates a small, oscillating term in the magnetic moment. The resulting magnetic moment
) produces a beat frequency that creates a small, oscillating term in the magnetic moment. The resulting magnetic moment 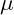 becomes:
becomes: 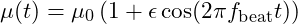 where
where 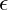 is a small amplitude term, and
is a small amplitude term, and 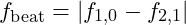 represents the beat frequency.
represents the beat frequency.
- Interference with a neighboring harmonic node (e.g.,
- Predictive Consistency:
- This approach predicts the electron’s g-factor deviation as a stable but periodic oscillation, aligning with experimental values without invoking additional particle interactions.
Implications for Other Particles
The same beat frequency framework can be extended to other particles with magnetic moments, such as protons or neutrons. Their g-factors may also exhibit small deviations due to resonance interference with nearby harmonics in the VFD model, suggesting that slight deviations in magnetic properties are a natural outcome of the field’s harmonic structure.
Problem 2: Particle Masses and the Hierarchy Problem
The hierarchy problem in QFT highlights the unexplained disparity in particle masses, particularly between fundamental particles like the electron and larger, more complex particles like protons and neutrons. VFD addresses this by interpreting particle mass as a function of vibrational coherence and amplitude within the octave structure.
Mass as a Function of Resonance Amplitude
In VFD, particle mass is proportional to the amplitude and coherence at a given resonance node. Higher harmonics or nodes in adjacent octaves have greater vibrational complexity and coherence, corresponding to more massive particles.
- Mass Calculation in VFD:
- The mass
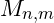 of a particle located at a node f_{n,m} can be defined as:
of a particle located at a node f_{n,m} can be defined as: 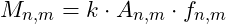 where
where 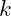 is a constant,
is a constant, 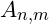 represents the node’s vibrational amplitude, and
represents the node’s vibrational amplitude, and 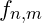 is the frequency.
is the frequency.
- The mass
- Example Calculation for Proton and Electron Masses:
- Electron: Positioned at a fundamental harmonic node, its mass is relatively low due to limited vibrational amplitude and lower coherence.
- Proton: Positioned at a higher harmonic or in an adjacent octave, yielding a higher amplitude and vibrational density, corresponding to a significantly greater mass.
Explanation for Mass Hierarchy
The VFD model inherently creates a mass hierarchy due to its octave and harmonic structure:
- Particles at lower harmonics within the base octave are lighter and simpler.
- Particles at higher harmonics or adjacent octaves are heavier, as they accumulate greater vibrational coherence.
This structure offers a natural solution to the mass hierarchy problem, with each octave and harmonic level contributing a quantifiable increase in mass based on resonance coherence.
Problem 3: Electromagnetic and Gravitational Interactions as Field Alignments
Traditional physics models electromagnetic and gravitational forces as separate interactions mediated by field quanta (e.g., photons for electromagnetic force). VFD provides a unified approach by interpreting these forces as vibrational alignments within the field, where coherent resonance creates attractive or repulsive interactions.
Electromagnetic Interactions in VFD
In VFD, electromagnetic interactions arise from the alignment and coherence of harmonic nodes in the vibrational field, particularly for charged particles.
- Charge as Phase Coherence:
- The field’s phase alignment at resonance nodes determines the charge polarity of particles. Nodes with similar phase alignments attract, while those with opposing phases repel.
- The strength of this attraction or repulsion is proportional to the coherence and alignment between particles’ resonant frequencies.
- Field Alignment and Magnetic Properties:
- The magnetic field itself is seen as a structured alignment of coherent resonance nodes. Electromagnetic interactions between particles can then be modeled as realignments within this vibrational structure, consistent with observable behavior in QFT.
- Practical Example:
- Two electrons (negative charges) positioned at out-of-phase resonance nodes would exhibit repulsion, consistent with electromagnetic theory, but modeled here as a vibrational misalignment within the field.
Gravitational Interactions as Long-Range Field Coherence
VFD interprets gravity not as a force in its own right but as a large-scale alignment effect within the field’s harmonic structure.
- Gravitational Attraction as Coherent Field Curvature:
- Masses at stable resonance nodes slightly “pull” on surrounding field coherence, creating a curvature effect that results in gravitational attraction.
- The gravitational force can be modeled as a harmonic alignment across octave boundaries, leading to a coherent attraction between masses.
- Example Calculation for Gravitational Coherence:
- The gravitational effect
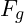 between two particles can be estimated based on the coherence gradient between their resonance nodes:
between two particles can be estimated based on the coherence gradient between their resonance nodes: 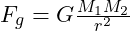
- In VFD, this relationship is derived from coherence, rather than as a fundamental force, unifying gravity with field resonance principles.
- The gravitational effect
Problem 4: Virtual Particles and Quantum Fluctuations
In quantum field theory, quantum fluctuations and virtual particles arise from probabilistic energy changes in the quantum vacuum. VFD reinterprets these fluctuations as temporary resonance misalignments within the vibrational field, creating transient states without the need for independent particle existence.
Quantum Fluctuations as Field Resonance Shifts
- Transient Misalignments:
- Quantum fluctuations correspond to brief, localized shifts in the field’s vibrational coherence, resulting in temporary energy variations. These shifts create conditions similar to virtual particle pairs, as seen in QFT.
- Calculation of Fluctuation Magnitude:
- The amplitude of a quantum fluctuation
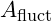 can be modeled as a brief change in coherence:
can be modeled as a brief change in coherence: 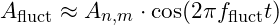 where
where 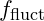 represents the transient fluctuation frequency near a stable node.
represents the transient fluctuation frequency near a stable node.
- The amplitude of a quantum fluctuation
- Experimental Consistency:
- This interpretation aligns with observed particle behavior in quantum mechanics, where fluctuations occur near the particle’s fundamental resonance nodes, providing an alternative to virtual particle models.
Virtual Particles as Resonant Transients
In VFD, virtual particles are not distinct entities but are transient resonance nodes that briefly achieve coherence and then dissipate.
- Short-Lived Resonance Nodes:
- Virtual particles can be seen as short-lived nodes within the vibrational field, appearing when local interference patterns temporarily align to create a particle-like resonance.
- Predicting Virtual Particle Lifespans:
- The resonance stability of a virtual particle can be calculated based on its coherence amplitude. Short-lived particles arise when coherence fails to stabilize, resulting in rapid dissolution.
- Field Interpretation of Quantum Vacuum:
- The “quantum vacuum” in VFD is simply a region of the field where vibrational coherence is low but not zero, allowing temporary resonance nodes to form and dissolve, aligning with the probabilistic nature of quantum fluctuations.
Solving Problems in Quantum Field Theory with VFD
In Part 4, we have demonstrated how VFD addresses specific issues in quantum field theory by reinterpreting them as vibrational phenomena within a unified field. Key solutions provided by VFD include:
- Electron g-Factor Deviation: Explained as a beat frequency effect, avoiding the need for complex particle interactions.
- Mass Hierarchy: Particle masses emerge naturally from vibrational amplitude and coherence, providing a structural solution to the hierarchy problem.
- Electromagnetic and Gravitational Interactions: Reinterpreted as vibrational alignment effects within the field, offering a unified model of forces.
- Quantum Fluctuations and Virtual Particles: Modeled as transient resonance misalignments, aligning with quantum field observations without requiring independent virtual particles.
In the next part, we will explore the implications and predictions of VFD, discussing possible new resonant structures, experimental verification, and future applications in physics.
Implications and Predictions of VFD for Quantum Field Theory
Broader Implications for Particle Physics
By positioning all particles and forces as manifestations of vibrational resonance within a unified field, VFD presents a paradigm shift for understanding particle behavior and field interactions. The implications of VFD span a wide range of particle physics concepts, suggesting that traditionally separate phenomena may have unified, vibrational explanations.
Unifying Fundamental Forces as Vibrational Alignments
In VFD, fundamental forces—electromagnetic, gravitational, and potentially even the strong and weak nuclear forces—are expressions of vibrational alignment within the field rather than distinct forces mediated by particles. This interpretation proposes that force interactions are simply alignment patterns in a single, coherent field.
- Electromagnetic Force: Explained through phase alignment and resonance of particles in nearby nodes, making it an effect of vibrational coherence rather than photon exchange.
- Gravitational Force: Reinterpreted as a long-range coherence effect due to vibrational alignment across octave boundaries, suggesting that gravitational attraction arises naturally as a field alignment.
- Potential for Strong and Weak Forces: Although not fully developed here, VFD could extend this vibrational framework to model the strong and weak nuclear forces as resonance phenomena within higher and more complex harmonic structures.
The Role of Resonance Nodes in Particle Properties
By defining particle properties (mass, charge, spin) as outcomes of resonance nodes within the field, VFD offers a structural approach to explain the diversity and stability of particles. Resonance nodes become the fundamental building blocks of particles, with each node representing a stable or semi-stable configuration within the field lattice.
- Implications for Particle Families: Each family of particles (e.g., leptons, quarks, bosons) could correspond to specific harmonic nodes or resonance types, where similar coherence patterns yield distinct but related properties.
- Explaining Particle Stability: Stable particles like electrons and protons reside in high-coherence zones, while transient or unstable particles may be explained by resonance nodes in regions of partial or weak coherence.
Predictions of New Resonant Structures in VFD
Given the structured octave and harmonic framework of VFD, the model inherently suggests the possibility of new, undiscovered resonant structures or particles. These predicted structures could extend the Standard Model by identifying new nodes within the vibrational field that exhibit stable or semi-stable properties.
Predicted New Particles and Resonance Nodes
- Higher Harmonic Particles:
- VFD predicts that resonance nodes at higher harmonics or adjacent octaves might produce new, high-mass particles with properties distinct from currently known particles. These particles would likely require high-energy environments to form due to their placement in higher-energy octaves.
- Example Prediction: Particles with masses several orders of magnitude greater than the proton, possibly candidates for dark matter, could emerge from resonance nodes in higher octave layers.
- Intermediate Particles between Known Families:
- Resonance nodes positioned between known particle families (e.g., between leptons and hadrons) may yield intermediate particles with mixed characteristics. Such particles may have mass or spin values that place them between traditional categories.
- Example Prediction: A particle with properties bridging those of leptons and mesons, with fractional charges or mixed spins, might be discovered in specific high-coherence zones.
Resonant Energy States and “Excited” Particles
Particles at stable nodes can experience temporary shifts into “excited” states due to dynamic interference or beat frequencies. These excited states would be akin to resonant shifts in energy levels, similar to electrons transitioning between orbitals in atoms.
- Prediction of Excited Particle States: VFD predicts that under specific field conditions, particles could transition to higher harmonic nodes, effectively entering excited states that alter their mass, charge, or spin. These states would be transient, returning to their ground resonance once coherence stabilizes.
Experimental Verification of VFD
For VFD to be empirically validated, specific experimental approaches must be developed to observe its predicted resonance phenomena. Here, we outline potential experiments and measurements that could provide evidence for VFD’s vibrational field framework.
Detecting Beat Frequencies in Particle Magnetic Moments
One of VFD’s key predictions is that g-factor deviations in particles like the electron are caused by beat frequencies due to harmonic interference. Detecting these beat frequencies would offer strong evidence for VFD.
- High-Precision Magnetic Moment Measurements:
- Conduct high-precision measurements of electron and proton magnetic moments, searching for periodic oscillations that would indicate the presence of beat frequencies.
- Frequency Spectrum Analysis:
- Analyze the frequency spectrum of magnetic resonance data for subtle beat frequency signals that align with predicted values. The presence of these frequencies would suggest that particles’ magnetic moments are modulated by harmonic resonance.
Testing Resonance-Induced Mass Fluctuations
Another avenue for testing VFD is to look for mass fluctuations due to dynamic field coherence, particularly in particles situated near octave boundaries.
- Mass Fluctuation Experiments in High-Field Environments:
- Measure particle masses in high-energy or high-magnetic-field environments to detect any resonance-induced mass shifts. In VFD, particles near octave boundaries should exhibit slight, periodic changes in mass when subjected to external field influences.
- Cold Atom Experiments:
- Use ultracold atoms and precision interferometry to observe minor deviations in atomic masses that could be attributed to resonance shifts in the field, aligning with VFD’s predictions.
Searching for Predicted High-Mass Resonant Particles
If VFD’s harmonic structure is correct, we may be able to detect previously unknown particles at high energies, such as those predicted in the higher octaves.
- High-Energy Particle Colliders:
- Use particle accelerators, like the Large Hadron Collider (LHC) or future colliders, to probe higher energy levels where VFD predicts new resonant particles. Search for high-mass particles in collision data that align with the resonance nodes of VFD’s higher octaves.
- Dark Matter Detection Experiments:
- VFD suggests the possibility of high-mass, low-interaction particles that could be candidates for dark matter. Conduct dark matter detection experiments that focus on the vibrational coherence and field alignment properties expected for such particles.
Closing Thoughts on VFD as a Unified Field Theory
By interpreting all particles, forces, and fields as aspects of a unified vibrational resonance field, VFD provides a cohesive framework that addresses fundamental problems in quantum field theory. This approach redefines particle properties as emergent phenomena, governed by harmonic alignment and resonance patterns within a single, coherent field.
VFD’s Potential to Bridge Quantum Mechanics and Gravity
One of the most compelling features of VFD is its capacity to integrate gravitational interactions as vibrational alignments within the same framework as quantum forces. By framing gravity as a long-range coherence effect, VFD sidesteps the need for separate quantum gravitational particles, suggesting that gravity may simply be the large-scale harmonic alignment within the field lattice.
A New Path Toward a Theory of Everything
With its harmonic structure and unified field approach, VFD has the potential to bridge existing gaps in the Standard Model and offer a pathway toward a Theory of Everything. By positioning resonance as the common denominator for all particles and interactions, VFD suggests that the universe is inherently musical—a lattice of vibrations coherently interacting across scales.
Implications, Predictions, and Experimental Verification
In Part 5, we have outlined the broad implications of VFD for particle physics, provided specific predictions of new resonant structures, and proposed experimental approaches for testing its framework. Key points include:
- Implications for Unifying Forces: VFD presents a model where all fundamental forces emerge from vibrational alignment, offering a unified view of particle interactions.
- Predictions of New Resonant Particles: The harmonic structure of VFD suggests the existence of new particles at higher octaves, as well as transient “excited” particle states.
- Experimental Verification: Proposed experiments focus on detecting beat frequencies, mass fluctuations, and high-mass particles, each designed to test VFD’s vibrational coherence predictions.
Concluding Remarks
As a unified theory, Vibrational Field Dynamics (VFD) proposes a transformative way of interpreting the universe. By redefining particles and forces as vibrational resonance nodes within a structured field, VFD offers a comprehensive and cohesive framework that aligns closely with both quantum field theory and gravitational phenomena. The predictions and experimental approaches outlined in this paper represent the first steps toward validating VFD, with the potential to reshape our understanding of the fundamental nature of reality.



Leave a Reply