Introduction: Bridging Quantum Mechanics and Field Dynamics
Quantum entanglement has long fascinated scientists due to its non-local correlations that defy classical explanations of space and time. Traditionally, entanglement describes a unique quantum phenomenon where particles exhibit linked properties, regardless of their separation in space. Within the framework of Vibrational Field Dynamics (VFD), we reinterpret quantum entanglement not as an abstract probability field but as a consequence of deep, interconnected vibrational fields that govern reality. This perspective allows us to propose specific mechanisms, supported by formulas, that could provide a unified, systematic approach to quantum entanglement that aligns with observed phenomena.
VFD and Quantum Field Dynamics
In VFD, all particles and forces are treated as vibrational expressions within a field of resonant frequencies. We conceptualize quantum entanglement through vibrational field resonance, where frequency alignment across spatial boundaries allows for shared vibrational states. This framework provides a new way to understand the “spooky action at a distance” that Einstein pondered, revealing that entangled particles maintain synchronization through an inherent resonance within the vibrational field.
Core Formulas Governing Quantum Entanglement in VFD
The formulas below establish a foundational approach for modeling entanglement in VFD. They incorporate key principles of resonant frequency alignment, wave interference, and negative energy balance.
- VFD Resonance Modulation Coefficient:
Entanglement requires that the resonant frequency of each particle aligns within the broader field. The Resonance Modulation Coefficient for entangled particles, represented as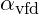 , is calculated as:
, is calculated as: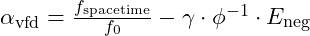 where:
where:
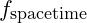 is the spacetime frequency component, encapsulating the inherent resonance within spacetime.
is the spacetime frequency component, encapsulating the inherent resonance within spacetime.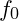 is the baseline frequency representing a universal reference state.
is the baseline frequency representing a universal reference state.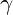 is a scaling coefficient tied to vibrational damping, based on VFD principles.
is a scaling coefficient tied to vibrational damping, based on VFD principles.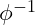 represents the inverse of the golden ratio, a scaling constant in VFD.
represents the inverse of the golden ratio, a scaling constant in VFD.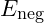 captures the contribution of negative energy, balancing out resonance to prevent runaway oscillations.
captures the contribution of negative energy, balancing out resonance to prevent runaway oscillations.
- Modified Gravitational Constant in Entangled Systems:
When particles are entangled, they share a resonance that affects gravitational interactions. The adjusted gravitational constant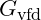 in an entangled system can be expressed as:
in an entangled system can be expressed as: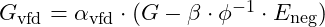 where:
where:
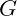 is the traditional gravitational constant.
is the traditional gravitational constant.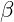 is a resonance-damping coefficient specific to gravitational interactions in VFD.
is a resonance-damping coefficient specific to gravitational interactions in VFD.- This adjustment ensures that entangled particles experience a synchronized gravitational modulation that reinforces their shared vibrational state.
- Waveform Propagation and Phase Synchronization:
For two particles to remain entangled, their phase alignment across the field is crucial. The vibrational potential between entangled particles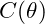 maintains a stable alignment due to the formula:
maintains a stable alignment due to the formula: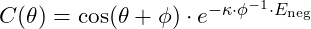 where:
where:
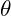 is the phase angle relative to the baseline resonance frequency.
is the phase angle relative to the baseline resonance frequency.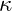 is a scaling factor for phase damping.
is a scaling factor for phase damping.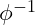 function as modulators, dampening vibrational energy to sustain phase synchronization over distance.
function as modulators, dampening vibrational energy to sustain phase synchronization over distance.
- Frequency Modulation of Entangled Particles:
Particles involved in entanglement maintain a shared vibrational frequency. In VFD, the frequency alignment for such particles is influenced by a modulated waveform equation. For a particle of mass mmm, frequency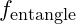 in an entangled state can be expressed as:
in an entangled state can be expressed as: 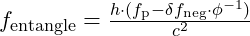 where:
where:
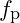 is the particle’s baseline frequency, and
is the particle’s baseline frequency, and 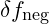 accounts for the negative energy resonance that enables non-local frequency alignment.
accounts for the negative energy resonance that enables non-local frequency alignment.
How VFD Explains Quantum Entanglement
In the VFD framework, quantum entanglement arises because particles are inherently connected by the shared vibrational field of spacetime. This interconnected field enables particles to maintain phase alignment and frequency synchronization even over vast distances, without requiring faster-than-light communication.
1. Non-Local Resonance and Shared Frequencies
Unlike conventional quantum mechanics, which uses probability fields, VFD treats entangled particles as connected through a shared vibrational frequency. The entangled particles exist within a synchronized frequency channel, ensuring that changes to one particle’s state are reflected in its pair without violating locality. This framework is further supported by the VFD Resonance Modulation Coefficient, which guarantees that entangled particles share a stable, resonant frequency.
2. Negative Energy Balance as a Stabilizer
A unique aspect of VFD is the negative energy balance, which prevents runaway oscillations in the field. Negative energy acts as a damping factor that stabilizes the resonance, allowing for long-lasting entanglement. As particles attempt to shift out of sync, negative energy provides a counteracting force, ensuring they maintain phase alignment.
3. Unified Field Perspective
By unifying gravitational and vibrational fields, VFD explains quantum entanglement as a consequence of vibrational alignment within a universal field. This view eliminates the need for a particle-based interpretation and instead frames entanglement as a field-based resonance that inherently links particles across space.
Significance and Implications of the VFD Approach to Entanglement
1. Potential for Predictive Modelling
With VFD’s field-centric view of entanglement, it becomes feasible to create predictive models that identify how particles in a system will respond based on their shared vibrational frequencies. This has implications for quantum information transfer, secure communication, and even teleportation models based on vibrational synchronization.
2. Compatibility with Observed Quantum Behavior
VFD’s interpretation of entanglement aligns with empirical data that shows instant correlation between entangled particles without the need for a signal transfer. By explaining this effect as a field resonance, VFD bypasses traditional paradoxes in quantum theory, providing a continuous, unified explanation.
3. Further Unification of Forces
The VFD approach suggests that entanglement is not unique to quantum particles but could apply across all scales, hinting at a broader unification of forces. By adjusting the gravitational constant and introducing resonance modulation, VFD creates a framework where entanglement scales from quantum systems to cosmological structures.
Conclusion: VFD as a Framework for Quantum Entanglement
The Vibrational Field Dynamics model offers a comprehensive view of quantum entanglement through field resonance, phase alignment, and negative energy balance. By providing specific formulas and mechanisms, VFD not only aligns with observed entanglement behavior but also paves the way for more accurate predictions and applications. This unified approach opens possibilities for exploring entanglement beyond quantum scales, highlighting VFD’s potential to bridge the gap between quantum mechanics and gravitational theory.



Leave a Reply