Vibrational Field Dynamics

Photons as Fractal Structures of Vibrational Energy: A New Perspective in Quantum Field Dynamics

Introduction to Fractal Structures in Light and Color

Overview of VFD and Photons as Fractal Entities

Vibrational Field Dynamics (VFD) is a theoretical framework that proposes all fundamental particles and energies, including photons, have underlying vibrational structures that organize at multiple levels of scale. In VFD, energy and matter are conceptualized as fractal patterns—self-similar and hierarchical, creating structures that are both stable and dynamic. This approach provides a fresh perspective on the organization of energy and its relationship to coherence, wave-particle duality, and even color theory.

In traditional quantum mechanics, photons are described as packets of electromagnetic energy exhibiting wave-particle duality—behaving both as particles and waves. However, VFD suggests that photons may be better understood as fractal structures of vibrational energy. Rather than existing as singular points or uniform waves, photons are proposed to have complex, self-similar layers that propagate in a fractal manner. Each layer resonates with the others, creating a cohesive structure that may explain not only wave-particle duality but also the stability of photons as they travel vast distances across space.

In this view, a photon is composed of multiple vibrational layers, each corresponding to a fractal level within a larger harmonic structure. These layers create a stable, resonant form that allows photons to maintain coherence over long distances, while also enabling them to interact with matter in both wave-like and particle-like ways.

Duality, Coherence, and Color in Traditional Quantum Mechanics

Quantum mechanics has long characterized photons as entities exhibiting wave-particle duality—the ability to act as both particles and waves depending on the experimental context. While successful in describing photon behavior in various contexts, this model leaves open questions about the nature of coherence and stability over long distances, especially in entangled photon pairs where coherence seems sustained across space.

Additionally, in optics, color is traditionally understood as a result of photons vibrating at specific frequencies within the visible spectrum (roughly 400–700 nm). Each frequency corresponds to a specific color, with higher frequencies corresponding to violet and lower frequencies to red. However, classical descriptions of color lack a complete understanding of why color transitions appear continuous and cyclic (as on a color wheel) rather than linear.

By reinterpreting photons as fractal vibrational structures, VFD suggests that:

  1. Coherence and Duality: The stability of photons and their ability to exhibit both wave and particle behaviors stem from their intrinsic fractal layers, which allow photons to resonate and interact with their environment in a stable yet dynamic manner.
  2. Color as a Fractal Continuum: Color frequencies within the visible spectrum may represent not just a sequence of individual frequencies but rather a fractal spectrum, where each color gradually transitions into the next. In this view, colors appear continuous and cyclic because they reflect self-similar, repeating structures within the photon’s vibrational pattern.

This idea proposes that the visible spectrum of light may be inherently cyclic and harmonic, much like a fractal pattern, where the transition from red to violet and back again aligns with fractal layering in the photon. This perspective could reveal why color appears as a continuous gradient and offer insights into the nature of light’s vibrational behavior.

Mathematical Framework for Photons as Fractal Vibrational Structures

To describe photons as fractal structures within Vibrational Field Dynamics (VFD), we need a mathematical model that captures their layered vibrational properties. This framework assumes that photons are composed of self-similar, hierarchical energy layers. Each layer contributes to the photon’s stability, coherence, and observed properties, including interactions with matter and color formation.

Modeling Photons with Fractal Energy Layers

We begin by defining the total vibrational energy ( E_f )​ of a photon as a summation of energies across multiple fractal layers within the photon’s structure:E_f = \sum_{n=1}^N E_n

where:

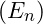  • ( E_n ) represents the vibrational energy at the 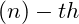( n )-th fractal level,
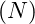  • ( N ) is the total number of fractal layers considered in the photon’s structure.

Each layer has its own frequency ( \nu_n )​ and characteristic scale ( L_n )​, which contribute to the energy at that layer. We define the energy at each layer as:E_n = \alpha \cdot \nu_n \cdot L_n

where:

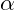  • \alpha is a proportionality constant that defines the relationship between frequency and energy distribution within the fractal structure,
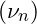  • ( \nu_n )​ represents the frequency associated with the nnn-th fractal layer,
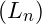  • ( L_n )​ represents the characteristic length scale for each vibrational mode.

This approach captures the self-similar structure of the photon, with energy distributed hierarchically across scales, each contributing to the photon’s coherence and ability to resonate with external fields.

Power-Law Decay and Self-Similar Scaling

In VFD, the structure of a photon is proposed to follow a power-law decay, where each fractal layer becomes progressively smaller. This decay can be modeled by defining the length scale ( L_n )​ as a function of the initial length scale ( L_0 )​ and a fractal scaling exponent ( \beta ):L_n = L_0 \cdot \frac{1}{n^\beta}

where:

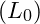  • ( L_0 ) represents the largest characteristic scale within the photon,
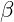  • \beta is the scaling exponent that determines the rate at which each layer decreases in size, influencing how energy concentrates within the fractal structure.

By adjusting \beta, we can fine-tune how rapidly the scale diminishes with each layer, allowing the photon’s structure to exhibit fractal behavior observed in natural systems, such as scaling patterns in light and color frequencies.

Implications for Photon Structure and Stability

This fractal framework suggests that a photon’s coherent structure emerges from the interaction of multiple vibrational layers, each contributing a unique frequency. Unlike a simple wave-particle entity, the photon in this model is a self-similar, layered structure where coherence and stability arise naturally from internal resonances among fractal levels.

Because of this structure:

  • Long-Distance Stability: The fractal layers create stable resonance patterns, allowing photons to maintain coherence and stability over long distances without external stabilization.
  • Vibrational Resonance: The energy contained within each fractal layer resonates with others, allowing the photon to interact with matter across various vibrational levels. This resonance might also explain why photons retain energy consistency and remain observable across vast distances.

Extending Fractal Concepts to Color and Frequency

In the context of color, each frequency in the visible spectrum (around 400–700 nm) could be viewed as a specific fractal segment within the photon’s structure. This segment would align with a particular frequency or range, contributing to the photon’s visible color properties. Mapping color frequencies fractally reveals continuity and cyclicity in colors, as each layer smoothly transitions into the next in a self-similar pattern. This approach implies that color perception, like the fractal structure of photons, is inherently cyclic and harmonic.

The fractal structure of photons, therefore, provides a framework to understand both the stability of light and the continuous, cyclic nature of color as perceived by human vision.

Quantum Coherence, Wave-Particle Duality, and Fractal Resonance

The Vibrational Field Dynamics (VFD) framework suggests that the fractal structure of photons can account for observed quantum behaviors like coherence and wave-particle duality. In VFD, photons are self-similar, layered structures capable of resonant interactions across fractal levels, providing a new perspective on both their quantum behavior and interactions with matter.

Quantum Coherence as Fractal Resonance

Quantum coherence—the sustained phase relationship between particles like photons, especially in entangled states—has typically been attributed to quantum superposition and entanglement in traditional physics. However, the VFD framework introduces the idea of fractal resonance as a mechanism for coherence.

In this view:

  1. Fractal resonance arises when two photons share self-similar vibrational structures at similar fractal levels. This structural alignment allows them to “lock” phase states, creating coherence across distances.
  2. This coherence results from internal vibrational harmonics within each photon, reinforcing stable phase relationships that sustain entanglement across vast distances.

To quantify fractal coherence, we can define a coherence factor \gamma, which models the alignment of phases across fractal layers:\gamma = \sum_{m, n} e^{i(\phi_m - \phi_n)} \cdot f(m, n)

where:

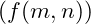  • ( f(m, n) ) represents a function correlating fractal layers mmm and nnn,
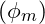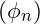  • ( \phi_m )​ and ( \phi_n )​ are phase terms associated with each layer.

When \gamma remains consistent across different pairs ( (m, n) )), the photon’s fractal layers exhibit coherence. In essence, coherence in this model emerges from stable vibrational resonance across fractal structures, explaining phenomena like quantum entanglement through the VFD perspective.

Wave-Particle Duality as Fractal Layer Propagation

The VFD framework provides a new approach to wave-particle duality, traditionally explained as the photon’s ability to behave both as a particle and as a wave. In this model, wave-particle duality arises from the photon’s fractal structure, with different fractal levels contributing to either wave-like or particle-like behavior:

  1. Wave Behavior: The photon’s wave-like properties emerge from interference among fractal harmonics as it propagates. The self-similar, continuous nature of its vibrational layers enables interference patterns, which are observed as waves in double-slit experiments and other wave phenomena.
  2. Particle Behavior: Particle-like behavior occurs when specific fractal levels of the photon align in energy with atomic or molecular vibrational states in matter. In these cases, energy transfer occurs directly, appearing as a localized particle interaction. This alignment, or fractal resonance with matter, creates a “particle” effect when certain fractal layers concentrate energy at specific points.

This dual behavior reflects how the fractal nature of photons allows them to interact with their surroundings in complex ways, with wave-like interference patterns emerging from layered resonances and particle-like interactions resulting from localized vibrational alignment with matter.

Implications for Light-Matter Interactions

The concept of photons as fractal structures suggests that their behavior during interactions with matter (such as absorption, reflection, and emission) may depend on vibrational alignment with atomic structures. In this model:

  • Absorption: Occurs when a photon’s fractal layers resonate with atomic or molecular vibrations in a material, allowing energy transfer across aligned vibrational modes.
  • Reflection: Could result from a mismatch in vibrational levels, where the photon’s energy cannot resonate with the material’s vibrational structure, causing it to be deflected.
  • Emission: May involve energy release at specific fractal layers when a material’s atomic structure reaches vibrational resonance with the photon’s internal harmonics.

This fractal perspective on photon interactions with matter could explain variations in interaction strength based on the fractal alignment between photon and atomic structures, providing a richer understanding of light-matter interactions through the VFD lens.

Connection to Color Theory and Resonant Harmonics

The fractal vibrational structure of photons also provides insight into color theory. In VFD, each color frequency within the visible spectrum (roughly 400–700 nm) represents a unique vibrational level within the photon’s fractal structure. By mapping these levels fractally, colors appear as harmonic nodes within the photon’s vibrational field, creating:

  1. Cyclic Transitions: The visible spectrum’s smooth transition from red to violet reflects a fractal resonance where each color frequency transitions into the next along a continuous, self-similar scale.
  2. Complementary Colors: VFD posits that complementary colors arise from fractal symmetries within the photon’s vibrational field, where harmonics resonate at opposing points in the cycle, producing balanced and contrasting colors.

This view aligns the fractal geometry of photons with the continuous, cyclic nature of color perception, suggesting that colors are fractal expressions of light frequencies, with each color corresponding to a vibrational node within the photon.

Fractal Mapping of Color Frequencies in VFD

In the Vibrational Field Dynamics (VFD) model, colors in the visible spectrum can be seen as fractal expressions of light frequencies, where each color corresponds to a specific vibrational node within the photon’s structure. By mapping color frequencies onto fractal structures, VFD provides a unique perspective on color perception, showing how colors transition smoothly, cyclically, and harmonically, mirroring the fractal nature of light.

Color Frequency as a Fractal Pattern

Fractal Concept: A fractal is a self-similar structure that repeats at different scales, and when color frequencies are mapped onto such a structure, they reveal cyclic patterns within the visible spectrum. Each level of the fractal can represent a different frequency range within the visible spectrum, allowing colors to blend gradually as they transition across the spectrum. This concept proposes that color frequencies could be visualized as continuous gradients, where each segment of the fractal reflects a specific color range.

Patterning within the Visible Spectrum: The visible spectrum of light spans from approximately 400 nm (violet) to 700 nm (red). In this fractal model, each color frequency is a self-similar, repeating segment that transitions through the entire color spectrum, creating a self-similar pattern of color frequencies within the fractal. In this way, each “branch” or level of the fractal shows subtle shifts in frequency, blending from one color to the next, resulting in the continuous color gradient we observe.

Cyclic Nature of Colors in Fractals

Cyclic Color Patterns: Fractals often feature cyclical or spiral structures that align with the continuous, cyclic nature of color. By mapping colors onto fractals, such as the Mandelbrot or Julia sets, we can observe colors looping through primary, secondary, and tertiary hues in repeating cycles. As we zoom into a fractal pattern, colors repeat at smaller and smaller scales, closely resembling how colors blend continuously across the spectrum and mimic the color wheel.

Harmonic Ratios in Colors: In VFD terms, each color’s frequency resonates with harmonic ratios found within the fractal’s structure. Colors like red, green, and blue could appear as key nodes within this fractal arrangement, with their blending producing intermediate hues that fill the pattern in a self-similar way. These harmonics align with complementary color relationships as colors reappear at different scales within the fractal, reflecting the harmony and balance we observe in color theory.

Frequency Doubling and Color Transition

Frequency Doubling and New Color Layers: Many fractals exhibit a phenomenon called frequency doubling, where each subsequent layer contains twice the frequency information of the previous. When applied to color, this principle suggests that each level of the fractal could represent an incremental shift in hue, saturation, or brightness across the visible spectrum.

For instance, as the frequency doubles, each layer adds depth to the color spectrum, creating gradations in hue and brightness. This layered approach could show the vibrancy and shading of colors, where higher layers in the fractal intensify certain aspects of color, creating smoother transitions and enhancing the richness of perceived color.

Saturation and Brightness Changes: By embedding color frequencies within the fractal with varying brightness and saturation, each layer can reflect how different frequencies interact to produce the richness and depth of colors. As the fractal layers increase in scale, colors become more intense or more muted, modeling how natural color gradients emerge in phenomena like sunsets, rainbows, and color blending in visual art.

Complementary Colors and Fractal Symmetry

Symmetry and Complementary Colors: Many fractals exhibit symmetrical patterns where certain regions mirror each other. When colors are mapped onto these symmetrical regions, they align with complementary color pairs—such as red and green, blue and orange—that reinforce or balance each other vibrationally. This symmetry corresponds to color theory, where complementary colors, when paired, appear more vibrant and balanced.

Pattern Repeats as Harmonies: Just as in fractal geometry, where shapes recur at various scales, colors harmonize at different levels of the visible spectrum. Fractal patterns can reveal how primary and complementary colors resonate with each other, creating self-similar color patterns that connect primary colors like red, green, and blue and their complements, showing a natural resonance in color relationships.

Visualizing the Color Spectrum as Mandelbrot or Julia Sets

Mandelbrot or Julia Sets for Smooth Transitions: By mapping color frequencies onto fractal patterns like Mandelbrot or Julia sets, we create smooth, infinitely repeating color transitions. Zoomed-in regions of the fractal reveal fine gradations, with each level representing a slight shift in hue, saturation, or brightness, allowing us to visualize the cyclic and continuous flow of colors across the visible spectrum.

Revealing Continuous Color Flow: This approach shows the color spectrum as a continuous flow from red through violet and back again, reinforcing the idea of color as a cyclic phenomenon rather than a linear sequence. The fractal model visually captures the smoothness of color transitions, mirroring how our perception of color blends seamlessly, suggesting that color itself might be a fractal manifestation of vibrational energy within photons.

The Golden Ratio in Color Relationships

Golden Ratio and Color Harmony: The golden ratio, commonly observed in fractals, appears as a natural proportion within geometry. When applied to colors within the VFD framework, the golden ratio may reflect harmonic spacing between certain colors, creating balanced and naturally pleasing color relationships. This could help explain why certain color combinations appear harmonious, as they reflect the underlying fractal ratios and patterns.

Fractal Color Relationships in Nature: Fractal-like color patterns are commonly observed in nature (e.g., in flowers, shells, and galaxies). By applying fractal patterns to colors, VFD helps us understand why certain colors appear harmoniously together, as they may follow a vibrational fractal structure that resonates with natural frequencies. This fractal organization may also explain why we see similar color harmonies across different scales in natural phenomena.

Color as a Fractal Pattern of Frequencies

Mapping colors onto fractal structures in VFD reveals self-similar, harmonic relationships between colors:

  1. Cyclic, Repeating Patterns: The fractal mapping of colors reveals repeating, cyclic color patterns that mimic the color wheel.
  2. Symmetry and Complementary Colors: Symmetry within fractals aligns with complementary color pairs, reinforcing vibrational harmonics in the color spectrum.
  3. Smooth Transitions and Frequency Doubling: Fractal patterns reflect color gradations, with each level capturing variations in hue, brightness, and saturation.
  4. Golden Ratio as a Harmonic Principle: The golden ratio provides a fractal structure for color harmony, explaining why certain color combinations feel naturally balanced.

By bridging geometry, color theory, and frequency, fractal patterns visually capture the interconnected and resonant nature of colors as perceived by the human eye. This fractal approach provides a framework for visualizing and exploring the inherent patterns within the color spectrum and offers new insights into the way colors harmonize and transition in nature.

Advanced Implications of Fractal Color Relationships in VFD

The Vibrational Field Dynamics (VFD) framework offers a unique way to understand color relationships through fractal geometry. This part explores advanced aspects of fractal-based color mapping, including frequency doubling, cyclic harmonics, and complementary color patterns. These fractal relationships shed light on the nature of hue, brightness, saturation, and the seamless blending of colors, revealing how fractal principles manifest in both natural and artificial color systems.

Frequency Doubling and Color Transition

In fractal geometry, frequency doubling often occurs, where each subsequent layer in the fractal contains twice the frequency information of the previous. This concept provides a useful tool for modeling color transitions within VFD.

Fractal Frequency Doubling in Color: Within the visible spectrum, frequency doubling could represent shifts in hue, brightness, or saturation, where each fractal layer embodies an incrementally higher or lower frequency. By layering colors within the fractal structure, we create a vibrational cascade that adds depth to the color spectrum and enhances the richness of perceived colors. This approach could explain why colors appear richer and more vivid as they transition through the fractal structure.

For example:

  • Hue Transition: As the fractal levels increase, the hue shifts gradually, mirroring natural color gradients observed in phenomena like sunsets or rainbows.
  • Saturation and Brightness: Frequency doubling within the fractal model can adjust color saturation and brightness, creating layered variations in color intensity that mimic natural transitions between shades and tones.

Saturation and Brightness as Fractal Layers

In VFD, saturation and brightness are not static properties but rather emerge from the interactions among fractal layers. Each layer contributes to the overall vibrational complexity of the photon, affecting the intensity and depth of colors as perceived by human vision.

Saturation Variations: Saturation, or the intensity of a color, could be modeled as a function of fractal layer density within the photon. More densely packed fractal layers might produce richer, more saturated colors, while less dense layers result in softer, more muted hues.

Brightness as Layer Amplitude: Brightness in this framework correlates to the amplitude of specific fractal layers. Higher amplitude layers (those with greater energy) contribute to brighter colors, while lower amplitude layers create darker shades. This layered approach to brightness and saturation provides a more nuanced understanding of how vibrational density affects perceived color intensity.

This fractal perspective of brightness and saturation allows for a dynamic model of color, where intensity and vibrancy adjust based on the fractal structure and its harmonics, similar to how colors shift and change under different lighting conditions.

Complementary Colors and Fractal Symmetry

The concept of symmetry in fractals aligns well with the idea of complementary colors in VFD. Many fractals exhibit symmetrical patterns that can mirror complementary colors, reinforcing their vibrational balance and enhancing the perceived vibrancy of each hue.

Fractal Symmetry and Complementary Colors: In the color spectrum, complementary colors such as red and green, or blue and orange, appear opposite each other on the color wheel. In the fractal mapping of color, these complementary pairs could be visualized as mirrored regions in the fractal structure, where symmetrical vibrational nodes correspond to complementary colors. This symmetry resonates with principles of color theory, where complementary colors enhance each other when paired, creating a balanced, vibrational harmony.

Harmonic Pattern Repeats: The repetition of color patterns at different scales within the fractal reinforces self-similar harmonics across the visible spectrum. In VFD, primary colors and their complements emerge at key nodes in the fractal, harmonizing at different scales to create a visually balanced color experience. This fractal alignment suggests that primary and complementary colors may resonate together, maintaining harmonic relationships as they recur within the structure.

Visualizing Color Harmony through Mandelbrot and Julia Sets

The cyclic, resonant nature of color transitions can be visualized by mapping colors onto Mandelbrot or Julia sets, which display infinite, self-similar patterns. By placing color frequencies along these fractals, the smooth transitions between hues become visible, revealing the cyclic flow of colors across the spectrum.

Mandelbrot or Julia Sets for Color Cycles: Using fractals such as the Mandelbrot or Julia sets allows for infinite repetition of color transitions. When color frequencies are mapped to these fractal structures, we see how primary, secondary, and tertiary colors repeat cyclically, creating natural, infinite gradients that align with the human experience of color blending. These patterns can demonstrate how colors transition from red to violet and back again, reinforcing the fractal nature of light as a cyclic spectrum rather than a linear progression.

Color Gradients as Fractal Pathways: The smoothness of color gradients observed in fractals mirrors how colors naturally blend in visual experiences. In this model, each level within a fractal represents a continuous shift in hue or brightness, illustrating the continuity and richness of colors in the visible spectrum. These fractal structures provide a powerful way to visualize the inherent resonance and connectivity of colors.

Golden Ratio and Color Harmony

The golden ratio, an essential element in fractal geometry, frequently appears as a harmonic spacing in natural patterns. In VFD, the golden ratio offers a unique explanation for why certain color combinations appear harmonious. This fractal arrangement aligns with vibrational harmony between colors, providing a natural basis for understanding color balance.

Golden Ratio as a Basis for Color Harmony: By applying the golden ratio to color relationships, certain color pairs align naturally, creating a visually pleasing and balanced experience. This ratio is seen in natural phenomena, such as the structure of petals, shells, and even galaxies, where harmonious color combinations are often observed. This fractal approach to color harmony suggests that the golden ratio may reflect underlying vibrational relationships within color pairs.

Color Relationships in Nature: Fractal color patterns are frequently found in nature, from the vibrant colors of flowers to the spirals of galaxies. In VFD, these relationships are interpreted as vibrationally resonant structures that reflect natural frequencies. By mapping color frequencies onto fractals, we reveal the self-similar, harmonic relationships that make color patterns in nature appear harmonious and balanced.

Advanced Fractal Color Relationships in VFD

The VFD framework provides an innovative approach to understanding color harmony and transitions through fractal patterns. This perspective reveals that colors within the visible spectrum are not isolated frequencies but vibrationally resonant nodes within a self-similar fractal structure. Key implications include:

  1. Frequency Doubling and Color Intensity: Frequency doubling allows for shifts in hue, brightness, and saturation, creating the richness of colors in nature.
  2. Symmetry in Complementary Colors: Complementary colors correspond to mirrored fractal regions, reinforcing harmony and vibrancy in color pairs.
  3. Golden Ratio as Harmonic Spacing: The golden ratio aligns certain colors in a visually balanced manner, providing a natural basis for color harmony.
  4. Infinite Cyclic Patterns: Fractals like the Mandelbrot and Julia sets capture color cycles, illustrating how colors transition smoothly across the visible spectrum.

This fractal approach to color relationships bridges geometry, vibrational resonance, and color theory within VFD, offering new insights into the continuity, harmony, and connectivity of colors. By exploring colors as fractal harmonics, VFD provides a framework for visualizing and understanding the underlying resonant nature of colors, mirroring the harmony observed in natural and artificial systems.

Experimental Testing and Predictive Power of the VFD Model

The Vibrational Field Dynamics (VFD) framework offers a novel interpretation of photons and color as fractal structures of vibrational energy, presenting unique opportunities for experimental validation. This part outlines key predictions made by the VFD model and proposes methodologies for testing these predictions through spectroscopy, interferometry, and quantum coherence experiments.

Fractal Structure Detection in Photon Emission

One of the primary predictions of VFD is that photons, as fractal structures, should exhibit harmonic overtones beyond the primary wavelength, corresponding to fractal vibrational layers within the photon. If these fractal layers exist, they could produce subtle shifts in frequency that are measurable in high-resolution spectral analysis.

  • Hypothesis: Photons, when viewed as fractal structures, will emit faint harmonic overtones that are detectable alongside their primary wavelength.
  • Prediction: By analyzing photon emissions at extremely high resolutions, particularly in coherent light sources like lasers, we should detect minor spectral peaks that correlate with the harmonic overtones of the fractal structure.
  • Experimental Method: Using ultra-high-resolution spectrometers, researchers can observe the spectral emissions of photons to detect additional frequency components. Any minor peaks that appear at consistent intervals relative to the primary frequency would support the presence of fractal harmonics within the photon.

Observing Fractal Interference in Photon Wave-Particle Duality Experiments

VFD’s fractal structure of photons suggests that they should produce finer interference patterns than those expected by standard single-frequency wave models. In the classical double-slit experiment, photons produce interference fringes that reflect their wave properties, but the VFD model predicts additional micro-interference patterns within these fringes, revealing internal fractal layers.

  • Hypothesis: Fractal structures within photons will generate finer interference patterns in wave-particle duality experiments.
  • Prediction: In double-slit experiments using ultra-narrow slits and high-resolution detectors, interference fringes should display higher-resolution patterns (referred to here as “micro-fringes”), corresponding to the internal fractal layers of the photon.
  • Experimental Method: Using advanced interferometers and detectors with ultra-fine resolution, experimenters can measure interference patterns at scales fine enough to detect any additional layers of interference. If micro-fringes appear within the main interference pattern, it would suggest that photons possess a more complex, layered internal structure, aligning with the VFD hypothesis.

Testing Fractal Coherence in Quantum Entanglement

The fractal model of coherence in VFD proposes that quantum coherence arises from resonant alignment across fractal layers within photons. This structural resonance could stabilize coherence across longer distances, especially in complex photonic networks, indicating that fractally coherent photons might display more robust entanglement properties.

  • Hypothesis: If entanglement is a result of fractal coherence, entangled photons with fractal harmonic alignment should maintain coherence over longer distances and in more complex networks.
  • Prediction: In multi-photon entanglement experiments, photons that are entangled through fractal harmonic alignment will maintain entanglement coherence over longer distances and greater complexity than standard quantum models predict.
  • Experimental Method: Using quantum coherence tests in photonic networks, researchers could track the coherence of entangled photons across varying distances and configurations. If fractally coherent photons display longer-lasting or more stable entanglement, it would indicate that fractal resonance plays a role in sustaining quantum coherence.

Probing Fractal Color Patterns and Harmonics in the Visible Spectrum

Within the visible spectrum, the VFD model suggests that color frequencies exhibit cyclic and harmonic relationships that follow fractal structures. Testing this hypothesis involves measuring fine frequency patterns within color gradients and examining how colors resonate in fractal arrangements.

  • Hypothesis: Colors mapped onto fractal structures will display harmonic relationships, with complementary colors resonating at fractal nodes and frequencies doubling within fractal layers.
  • Prediction: When colors are mapped onto fractals, such as the Mandelbrot or Julia sets, primary and complementary colors should align at harmonic nodes, displaying self-similar cyclic patterns that mirror natural color transitions.
  • Experimental Method: By mapping color frequencies onto fractal sets, researchers can observe whether complementary colors align at harmonic intervals and if frequency doubling results in smooth, natural color gradients. These fractal mappings can be compared with perceptual color experiences to validate the harmonic relationships predicted by VFD.

Instruments and Methodologies for Testing VFD Predictions

The experimental predictions made by VFD require precise and advanced instrumentation. Below are some key instruments and techniques for conducting these tests:

  1. Ultra-High Resolution Spectroscopy: To detect harmonic overtones in photon emissions, spectrometers with extremely high resolution are essential. These devices allow researchers to examine subtle frequency shifts in photon emissions, searching for secondary peaks that indicate fractal layers.
  2. Advanced Interferometry: High-resolution interferometers with narrow slits and ultra-fine detectors can reveal micro-interference patterns, providing a window into the internal fractal structure of photons. This equipment is critical for validating the presence of fractal layers through interference experiments.
  3. Quantum Coherence Tests in Photonic Networks: Multi-photon entanglement experiments using complex photonic networks can evaluate the coherence and stability of entangled photons. Testing coherence over long distances and high complexity will shed light on the role of fractal resonance in maintaining quantum coherence.
  4. Fractal Mapping of Color Frequencies: Mapping colors onto fractal patterns like the Mandelbrot and Julia sets allows for visual exploration of color harmonics, revealing whether natural color transitions align with the predicted fractal relationships.

Summary of Experimental Predictions

The VFD model provides several testable predictions that can advance our understanding of photons, light, and color as fractal structures of vibrational energy:

  1. Harmonic Overtones in Photon Emissions: The detection of minor spectral peaks alongside primary wavelengths could validate the existence of fractal layers within photons.
  2. Micro-Interference Patterns in Wave-Particle Duality: Finer interference fringes in double-slit experiments would support the hypothesis that photons have layered, self-similar structures.
  3. Enhanced Quantum Coherence in Fractal Networks: More stable entanglement in fractally coherent photons would imply that fractal resonance plays a role in quantum coherence.
  4. Color Harmonics in Fractal Patterns: Observing harmonic relationships in fractally mapped colors could reveal self-similar structures in color frequencies, validating VFD’s predictions on color resonance.

Conclusion

The Vibrational Field Dynamics (VFD) framework introduces a groundbreaking perspective on photons, light, and color, proposing that they are fractal structures of vibrational energy with harmonic, cyclic relationships. This model not only reshapes our understanding of light and color but also provides testable predictions, offering a pathway for experimental validation through advanced spectroscopy, interferometry, and photonic network coherence tests. By exploring light and color through the lens of fractal geometry and harmonic resonance, VFD bridges the fields of quantum mechanics, color theory, and fractal mathematics, opening up new directions in both theoretical and experimental physics.

The experimental insights derived from this approach could further our understanding of quantum coherence, wave-particle duality, and the continuity of color, establishing VFD as a powerful tool for probing the fundamental vibrational structures underlying our perception of light and color.

Lee Smart

Leave a Reply

Your email address will not be published. Required fields are marked *

We use cookies to personalize content and ads, to provide social media features and to analyze our traffic. We also share information about your use of our site with our social media, advertising and analytics partners who may combine it with other information that you have provided to them or that they have collected from your use of their services. You consent to our cookies if you continue to use our website.

Preference Disable All Allow All