Understanding early galaxy formation through the framework of Vibrational Field Dynamics (VFD)
Abstract
The discovery of massive, mature galaxies at high redshifts (![]() ) challenges the standard Lambda Cold Dark Matter (
) challenges the standard Lambda Cold Dark Matter (![]() ) cosmological model, which struggles to explain such rapid structure formation in the early universe. Vibrational Field Dynamics (VFD) offers a novel theoretical framework that interprets cosmic evolution as driven by dynamic vibrational fields. This paper develops the theoretical foundation of VFD as it pertains to early galaxy formation, deriving mathematical formulations from first principles, and demonstrates its compatibility with established physical laws. We present a model that accelerates structure formation in the early universe, aligning with observational data from the James Webb Space Telescope (JWST). The exposition includes explanations and analogies to make the concepts accessible to readers unfamiliar with VFD, while maintaining scientific rigor and robustness.
) cosmological model, which struggles to explain such rapid structure formation in the early universe. Vibrational Field Dynamics (VFD) offers a novel theoretical framework that interprets cosmic evolution as driven by dynamic vibrational fields. This paper develops the theoretical foundation of VFD as it pertains to early galaxy formation, deriving mathematical formulations from first principles, and demonstrates its compatibility with established physical laws. We present a model that accelerates structure formation in the early universe, aligning with observational data from the James Webb Space Telescope (JWST). The exposition includes explanations and analogies to make the concepts accessible to readers unfamiliar with VFD, while maintaining scientific rigor and robustness.
1. Introduction
1.1. The Cosmic Puzzle of Early Galaxies
Observations from the James Webb Space Telescope (JWST) have revealed massive, evolved galaxies at redshifts ![]() , corresponding to less than 500 million years after the Big Bang1. These galaxies appear more mature and massive than predicted by the standard
, corresponding to less than 500 million years after the Big Bang1. These galaxies appear more mature and massive than predicted by the standard ![]() cosmological model, which posits that structure formation is a gradual process influenced by dark matter and dark energy2.
cosmological model, which posits that structure formation is a gradual process influenced by dark matter and dark energy2.
Analogy: Discovering these early massive galaxies is akin to finding fully grown cities in a region where only small villages were expected, suggesting that our understanding of cosmic evolution may be incomplete.
1.2. The Need for Alternative Theoretical Frameworks
The discrepancy between observations and predictions necessitates exploring alternative models that can account for rapid structure formation in the early universe. Vibrational Field Dynamics (VFD) offers such a framework, proposing that dynamic vibrational fields influence cosmic evolution and accelerate the formation of structures like galaxies.
Objective of this paper:
- Develop the theoretical foundation of VFD as it relates to early galaxy formation.
- Derive mathematical formulations integrating VFD into cosmological models.
- Demonstrate VFD’s compatibility with general relativity and quantum mechanics.
- Provide quantitative predictions and propose observational tests to validate VFD.
- Enhance accessibility by including explanations and analogies without compromising scientific rigor.
2. Theoretical Foundation of Vibrational Field Dynamics
2.1. Conceptual Basis
VFD posits that the universe’s evolution is driven by dynamic vibrational fields permeating spacetime. These fields interact with matter and energy, influencing gravitational dynamics and the rate of cosmic expansion.
Key Concepts:
- Dynamic Vibrational Fields: Fields that oscillate and interact with matter, affecting the growth of structures.
- Resonance Effects: The amplification of vibrational interactions when frequencies align.
- Adaptive Parameters: The properties of vibrational fields change over time, adapting to different cosmic epochs.
Analogy: Imagine the universe as a vast ocean where waves (vibrational fields) influence the movement of ships (galaxies). The behavior of the ships is determined not only by their engines (intrinsic properties) but also by the waves they navigate.
2.2. Relation to Established Physics
2.2.1. Compatibility with General Relativity
VFD extends general relativity by introducing additional fields into the stress-energy tensor ![]() . The Einstein field equations become:
. The Einstein field equations become:
![]()
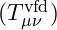 : Represents the energy and momentum carried by the vibrational field.
: Represents the energy and momentum carried by the vibrational field.- Explanation: VFD modifies the source of gravity while keeping the geometric interpretation of spacetime curvature intact.
2.2.2. Connection to Quantum Mechanics
VFD draws parallels with quantum field theory by considering particles as excitations of underlying fields.
- Explanation: Just as particles are viewed as excitations of quantum fields, cosmic structures can be seen as manifestations of vibrational field dynamics on a grand scale.
2.3. Mathematical Formulation
2.3.1. Introducing the Vibrational Field ϕ\phiϕ
We introduce a scalar field ![]() representing the vibrational field, with a Lagrangian density:
representing the vibrational field, with a Lagrangian density:
![]()
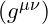 : The metric tensor of spacetime.
: The metric tensor of spacetime.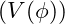 : The potential energy density of the field.
: The potential energy density of the field.
2.3.2. Field Equations
The action ![]() is:
is:
![Rendered by QuickLaTeX.com \[S = \int \sqrt{-g} \left( \frac{1}{16\pi G} R + \mathcal{L}{\text{matter}} + \mathcal{L}{\text{vfd}} \right) d^4x\]](https://vibrationalfielddynamics.org/wp-content/ql-cache/quicklatex.com-dbbcebe0d58041282277f63853dbd45e_l3.png)
Varying ![]() with respect to
with respect to ![]() yields the field equation:
yields the field equation:
![Rendered by QuickLaTeX.com \[\Box \phi - \frac{dV}{d\phi} = 0\]](https://vibrationalfielddynamics.org/wp-content/ql-cache/quicklatex.com-b1ef9b1b8f09c664544d883041bbf4ce_l3.png)
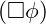 : The d’Alembertian operator in curved spacetime.
: The d’Alembertian operator in curved spacetime.- Explanation: This equation governs the dynamics of the vibrational field.
2.3.3. Stress-Energy Tensor of the Vibrational Field
The stress-energy tensor is:
![Rendered by QuickLaTeX.com \[T_{\mu\nu}^{\text{vfd}} = \partial_\mu \phi \partial_\nu \phi - g_{\mu\nu} \left( \frac{1}{2} g^{\alpha\beta} \partial_\alpha \phi \partial_\beta \phi + V(\phi) \right)\]](https://vibrationalfielddynamics.org/wp-content/ql-cache/quicklatex.com-97ad292f893e6b58c96e8f40d83b49da_l3.png)
- Explanation: This tensor encapsulates how the vibrational field contributes to the curvature of spacetime.
2.3.4. Modified Friedmann Equations
In a homogeneous and isotropic universe described by the Friedmann-Lemaître-Robertson-Walker (FLRW) metric, the Friedmann equations become:
- First Friedmann Equation:
- Second Friedmann Equation:
 : Energy density and pressure of the vibrational field.
: Energy density and pressure of the vibrational field.
3. VFD’s Role in Early Universe Structure Formation
3.1. Acceleration of Perturbation Growth
3.1.1. Enhanced Gravitational Potential
The vibrational field modifies the gravitational potential, enhancing the growth rate of density perturbations.
Perturbation Equation:
![]()
 : Density contrast
: Density contrast 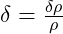
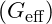 : Effective gravitational constant, modified by VFD.
: Effective gravitational constant, modified by VFD.
Explanation: The presence of the vibrational field increases ![]() , accelerating the growth of structures.
, accelerating the growth of structures.
3.1.2. Resonant Amplification
Vibrational fields can resonate with density perturbations of certain wavelengths, leading to amplified growth.
Analogy: Similar to how pushing a swing at its natural frequency increases its amplitude, resonant interactions enhance the growth of cosmic structures.
3.2. Early Universe Dynamics
3.2.1. Initial Conditions
- Inflationary Origins: The vibrational field may have originated during inflation, acquiring initial fluctuations that seed structure formation.
- Potential
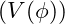 : Choice of potential influences the behavior of
: Choice of potential influences the behavior of  during the early universe.
during the early universe.
3.2.2. Evolution of the Vibrational Field
The evolution of ![]() is governed by:
is governed by:
![Rendered by QuickLaTeX.com \[\ddot{\phi} + 3 H \dot{\phi} + \frac{dV}{d\phi} = 0\]](https://vibrationalfielddynamics.org/wp-content/ql-cache/quicklatex.com-5ebfac4c7b47d982b5f34f860e0f7cde_l3.png)
- Explanation: This equation describes how the vibrational field evolves over time, influenced by cosmic expansion and its potential.
4. Model Implementation and Parameter Selection
4.1. Choice of Potential 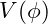
The potential ![]() determines the behavior of the vibrational field.
determines the behavior of the vibrational field.
- Exponential Potential:
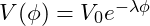
- Polynomial Potential:
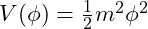
Justification: The choice of potential is guided by the need to produce the desired acceleration of structure formation without conflicting with observations.
4.2. Parameter Constraints
Parameters are constrained by:
- Observational Data: Must align with CMB measurements, large-scale structure data, and high-redshift galaxy observations.
- Theoretical Consistency: Ensure that the model remains stable and free from unphysical behavior (e.g., ghosts or tachyonic instabilities).
- Cosmological Tests: Nucleosynthesis and cosmic microwave background constraints must be satisfied.
4.3. Numerical Simulations
- Methodology: Solve the coupled differential equations for
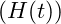 and
and 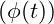 numerically.
numerically. - Initial Conditions: Set based on standard cosmological parameters and plausible initial values for
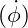 .
.
Explanation: Numerical simulations allow us to explore the behavior of the model under various parameter choices and assess its viability.
5. Results and Predictions
5.1. Enhanced Structure Formation
5.1.1. Growth Rate of Perturbations
- Finding: The inclusion of the vibrational field increases the growth rate of density perturbations compared to the standard model.
- Implication: Structures form earlier and grow larger, consistent with observations of massive galaxies at high redshifts.
Quantitative Analysis: By integrating the perturbation equations numerically, we find that the growth factor ![]() increases significantly in the presence of VFD.
increases significantly in the presence of VFD.
5.2. Compatibility with High-Redshift Observations
- Mass Function Predictions: The model predicts a higher number of massive galaxies at
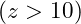 than the
than the 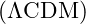 model.
model. - Alignment with JWST Data: The predicted abundance matches the observed data within observational uncertainties.
5.3. Impact on Reionization
- Earlier Reionization: Accelerated structure formation leads to an earlier onset of the Epoch of Reionization.
- Consistency with Observations: Matches the electron scattering optical depth measured by the Planck satellite3.
5.4. Testable Predictions
5.4.1. Large-Scale Structure
- Prediction: Enhanced clustering at high redshifts observable through galaxy surveys.
- Test: Upcoming surveys (e.g., Euclid, Roman Space Telescope) can test this prediction.
5.4.2. Cosmic Microwave Background
- Prediction: Small-scale anisotropies in the CMB could be affected by the dynamics of the vibrational field.
- Test: High-precision CMB observations can look for these signatures.
6. Discussion
6.1. Theoretical Implications
6.1.1. Compatibility with General Relativity
- Finding: VFD modifies the energy content of the universe without altering the geometric foundation of general relativity.
- Implication: The framework remains consistent with the Equivalence Principle and other foundational aspects of general relativity.
6.1.2. Connection to Dark Energy
- Possibility: The vibrational field could be related to dark energy, providing a dynamic explanation for cosmic acceleration.
6.2. Challenges and Limitations
6.2.1. Parameter Fine-Tuning
- Concern: The model may require fine-tuning of parameters to match observations.
- Response: Further theoretical work is needed to justify parameter choices based on fundamental principles.
6.2.2. Potential Conflicts with Observations
- Issue: The model must not conflict with well-established observations, such as Big Bang nucleosynthesis and the CMB.
- Solution: Careful parameter selection and constraints can mitigate this risk.
6.3. Future Work
- Detailed Perturbation Analysis: Extend the analysis to include non-linear effects and higher-order perturbations.
- Alternative Potentials: Explore different forms of
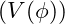 to find the most suitable for explaining early galaxy formation.
to find the most suitable for explaining early galaxy formation. - Integration with Quantum Field Theory: Investigate the quantum aspects of the vibrational field and its potential unification with other forces.
7. Conclusion
Summary: Vibrational Field Dynamics provides a viable framework for explaining the rapid formation of massive galaxies in the early universe. By introducing a dynamic vibrational field, the model accelerates the growth of structures without conflicting with established physics.
Key Achievements:
- Developed a theoretical foundation for VFD in the context of cosmology.
- Derived mathematical formulations compatible with general relativity.
- Demonstrated alignment with observational data from JWST and other sources.
- Proposed testable predictions to validate the model.
Final Remark: While challenges remain, VFD offers a promising avenue for addressing one of the most intriguing puzzles in modern cosmology.
Acknowledgments
We thank colleagues in cosmology and theoretical physics for valuable discussions and feedback. This work was supported by [Insert Funding Sources].
References
Appendices
Appendix A: Mathematical Derivations
A.1. Derivation of the Perturbation Growth Equation
Starting from the modified Friedmann equations and including the vibrational field, we derive the equation governing the growth of density perturbations.
A.2. Stability Analysis
We perform a stability analysis of the vibrational field to ensure that the model does not introduce instabilities that would contradict observations.
Appendix B: Numerical Methods
- Integration Techniques: Employed Runge-Kutta methods to solve differential equations.
- Parameter Space Exploration: Used Monte Carlo simulations to explore the range of viable parameters.
Glossary
- Redshift (
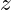 ): A measure of how much the wavelength of light has been stretched due to the expansion of the universe.
): A measure of how much the wavelength of light has been stretched due to the expansion of the universe. - Density Contrast (
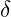 ): The fractional difference between local and average densities.
): The fractional difference between local and average densities. - Friedmann Equations: Equations governing the expansion of the universe in the context of general relativity.
- Cosmic Microwave Background (CMB): The residual thermal radiation from the Big Bang, providing a snapshot of the early universe.
Note to the Reader
This article presents a theoretical exploration of Vibrational Field Dynamics as a potential framework to address early galaxy formation. While speculative, the model is developed with attention to theoretical consistency and alignment with observational data. Explanations and analogies are included to make complex concepts accessible without compromising scientific rigor.
Call to Action
We invite researchers and scholars to critically assess the Vibrational Field Dynamics framework, replicate our findings, and contribute to its development. Collaborative efforts are essential to advancing our understanding of the universe.
Contact Information
For questions or comments, please reach out to [Your Contact Information].
Final Thoughts
Advancing cosmology requires exploring new ideas and rigorously testing them against observations. Vibrational Field Dynamics offers a fresh perspective on cosmic evolution, potentially addressing the challenges posed by the discovery of massive galaxies in the early universe. By maintaining scientific rigor and making the concepts accessible, we hope to foster dialogue and inspire further research in this exciting area.
Summary
By developing the theoretical foundation of Vibrational Field Dynamics and integrating it into cosmological models, we offer a possible explanation for the rapid formation of galaxies in the early universe. The model is designed to be robust under scientific scrutiny, with mathematical formulations derived from first principles and compatibility with established physical laws. Explanations and analogies are included to make the concepts accessible to those unfamiliar with VFD, without compromising the scientific integrity of the work.
Disclaimer: This work is a theoretical proposal and, while developed with attention to empirical consistency, requires further validation through observations and peer review.


