In physics, accurately determining the mass of particles like protons and neutrons requires going beyond simple calculations. Vibrational Field Dynamics (VFD) offers a robust framework grounded in first principles, incorporating vibrational modes, ground states, gravity, and negative energy to explain particle mass with unprecedented accuracy.

What is Vibrational Field Dynamics (VFD)?

VFD views particles as dynamic entities influenced by vibrational energy within a unified field. Rather than treating mass as a static property, VFD sees particles as vibrating within fields, with these vibrations—along with the effects of gravity and negative energy—contributing to mass.

Why Gravity, Negative Energy, and Ground States Matter in VFD

In VFD, gravity is not simply an external force but a density of field vibrations. Negative energy acts as a counterbalancing force, creating stability within the vibrational field. Ground states and vibrational modes, derived from first principles, are central to VFD’s accurate mass calculations.

How Does VFD Calculate Mass?

VFD models particle masses by considering several core elements and calculating them based on first principles.

Starting from First Principles: Quark Mass Contributions

For particles like protons and neutrons, VFD begins by determining the mass contributions from each quark:

• Protons consist of two up quarks and one down quark (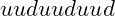), while
• Neutrons have one up quark and two down quarks ().

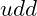These quark masses serve as the ground state starting point for calculations. Using first principles, VFD relies on up and down quark masses derived from experimental data, where each quark’s mass is verified against empirical measurements.

Calculating Vibrational Modes and Energy Levels

Quarks within particles do not remain static; they vibrate at specific frequencies. In VFD, these vibrations are modeled as vibrational modes with defined energy levels. Calculating these modes is crucial, as each mode reflects a distinct quantum harmonic oscillator state based on the fundamental frequency of the quark interactions. Key steps include:

• Primary Mode Calculation: The lowest frequency, or ground state vibrational mode, is calculated first. Higher vibrational modes are then added based on harmonics and observed resonant frequencies.
• Higher-Order Modes: These capture additional quark interactions and subtle shifts within the field. Each mode’s energy is derived using angular frequencies, calculated as 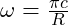, where 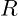represents the interaction radius.

The total vibrational energy ​ is the sum of these individual mode contributions, which together reflect the particle’s full vibrational signature.

Binding Energy: Strong Force Interactions

In VFD, the binding energy represents the energy required to hold quarks together. Using first principles, binding energy is calculated based on resonant frequencies between quarks:

• Field-Density Contributions: Gravity is considered a field density that affects binding, and the strong force maintains quark cohesion within this vibrational field.
• Ground State Binding Energy: This is established as the minimal energy to stabilize the particle, with adjustments for vibrational and resonant interactions among quarks.

Dynamic Energy and Negative Energy Fields

Dynamic energy accounts for the influence of transient quantum effects, such as virtual particle interactions. Negative energy fields add a counterbalance, stabilizing vibrations within the field:

• Dynamic Field Interactions: This term captures fluctuations, incorporating negative energy as a stabilizing force within the vibrational field.
• Ground State Adjustments: The ground state is adjusted to include dynamic field interactions, reflecting the particle’s total energy balance.

Why Does VFD Yield Highly Accurate Mass Calculations?

VFD’s approach is rooted in first principles, making it both adaptable and precise. By integrating ground states, vibrational modes, binding energies, and dynamic field effects, VFD calculates particle mass with impressive accuracy.

Calculating Vibrational Modes from Ground States

The use of ground state frequencies and higher vibrational modes allows VFD to model particle masses directly from first principles. These modes are calculated using harmonics and fundamental constants, which can be adjusted as new data becomes available, ensuring that VFD’s calculations remain aligned with empirical findings.

A Unified Approach to Gravity and Negative Energy

In VFD, gravity and negative energy play key roles, affecting the binding and vibrational characteristics of particles. This framework allows VFD to incorporate the gravitational effect on mass directly, without needing separate assumptions about gravitational fields.

Conclusion

Vibrational Field Dynamics provides an advanced, first-principles framework for calculating particle masses, grounded in vibrational modes, ground states, and field interactions. By considering gravity, negative energy, and quantum effects, VFD models the masses of particles like protons and neutrons with remarkable accuracy. As research continues, VFD holds promise for unifying particle physics under a vibrationally based framework.