Author: Lee Smart
Introduction
The notion of a unified framework that explains stability across scales—from subatomic particles to cosmic structures—has long been a fundamental goal in theoretical physics. Traditional approaches have explained atomic stability primarily through strong nuclear forces, electromagnetic interactions, and quantum mechanics, while cosmic structures like planetary orbits are governed by gravitational forces in the framework of classical mechanics and general relativity. Despite the progress achieved by these theories, a unified description that captures both atomic and cosmic stability remains elusive.
This paper introduces a novel theoretical framework based on Vibrational Field Dynamics (VFD), which suggests that the stability of atomic and cosmic structures is fundamentally governed by frequency-based interactions. At its core, VFD proposes that frequency scaling and harmonic resonance create stability nodes where balanced forces manifest, giving rise to persistent structures such as atomic nuclei and planetary systems. This approach seeks to bridge the gap between atomic and cosmic stability by considering both positive and negative forces as frequency-driven dynamics that organize matter through stable vibrational nodes.
Our model introduces new mathematical concepts that incorporate frequency-based scaling, negative energy influence, harmonic expansion, and golden ratio symmetry. By applying these principles to atomic nuclei and planetary orbits, we propose a framework that may provide answers to longstanding questions in physics, such as the nature of atomic stability at “magic numbers” and the harmonics that underlie planetary spacing. This frequency-based model opens avenues for predicting stable configurations in nuclear physics and potentially offers insights into the formation of stable planetary orbits within the solar system.
In this first part of the paper, we lay the foundation for VFD by introducing the concept of frequency scaling using the golden ratio and establishing the initial mathematical framework for stability nodes. We introduce the role of negative energy as a stabilizing influence and outline how harmonic resonance can yield stability in atomic and cosmic contexts. This section serves as the conceptual groundwork for the unified stability function, which we explore in greater mathematical detail in subsequent parts.
Introduction to Vibrational Field Dynamics (VFD) and Resonance Principles
Vibrational Field Dynamics and the Concept of Frequency-Based Stability
In Vibrational Field Dynamics (VFD), frequency and vibrational resonance are viewed as the primary drivers of stability in atomic and cosmic structures. Unlike conventional theories, where stability is explained by individual forces like nuclear attraction or gravitational pull, VFD suggests that all structures emerge from a fundamental vibrational field. Within this field, stability is achieved at specific frequency nodes, which act as “anchors” for stable configurations. These nodes arise from the constructive interference of waves within the field, resulting in persistent structures, be they atomic nuclei or planetary orbits.
In this model, each structural component—proton, neutron, or celestial body—exists as a vibrational mode that resonates within the larger field. By applying frequency scaling to these vibrational modes, VFD provides a systematic way to calculate stability points where these structures naturally arise and persist. This view transforms stability from a force-driven phenomenon to a resonance-based interaction governed by harmonic intervals.
Harmonic Nodes and the Golden Ratio in Frequency Scaling
One of the central tenets of VFD is that harmonic nodes, or points of stability, can be predicted through frequency scaling based on the golden ratio ![]() . The golden ratio, approximately 1.618, is a well-known constant that appears in natural patterns, fractals, and stable structures across multiple scales. In VFD, we postulate that stable configurations—such as atomic nuclei with specific neutron-proton counts and orbital positions in planetary systems—arise at these harmonic nodes.
. The golden ratio, approximately 1.618, is a well-known constant that appears in natural patterns, fractals, and stable structures across multiple scales. In VFD, we postulate that stable configurations—such as atomic nuclei with specific neutron-proton counts and orbital positions in planetary systems—arise at these harmonic nodes.
To mathematically describe these resonance nodes, we define the fundamental frequency scaling equation as follows: ![]()
where:
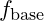 is a base frequency that represents a foundational vibrational energy in the field,
is a base frequency that represents a foundational vibrational energy in the field, is the golden ratio
is the golden ratio 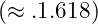 ,
,- nnn is an integer that represents the node number in the harmonic sequence.
This scaling framework creates a predictable pattern of stable nodes across frequency intervals, aligning with observed stability patterns in both atomic structures (such as magic numbers) and planetary orbits. The use of the golden ratio as a scaling constant suggests that self-similarity and fractal geometry underpin the stability of structures across scales, an idea that resonates with observations of natural stability patterns.
Negative Energy as a Stabilizing Influence
Another distinctive feature of VFD is the concept of negative energy as a stabilizing force that counterbalances the positive forces in atomic and cosmic structures. While positive forces drive attraction and cohesion, particularly in nuclear and gravitational contexts, negative energy provides a modulating effect that prevents excessive energy accumulation and destabilization. In this sense, negative energy serves as a frequency-dependent stabilizer, with its influence diminishing as frequency increases.
We define the negative energy influence function as follows:![]()
where:
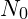 is a constant representing the base level of negative energy influence,
is a constant representing the base level of negative energy influence,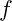 is the frequency at a given node,
is the frequency at a given node,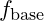 is the foundational frequency,
is the foundational frequency,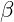 is an exponent governing the scaling of negative energy with frequency,
is an exponent governing the scaling of negative energy with frequency,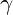 is a decay constant that modulates the influence of negative energy at higher frequencies.
is a decay constant that modulates the influence of negative energy at higher frequencies.
This equation captures the inverse relationship between negative energy influence and frequency, where lower frequencies receive more stabilizing influence. This relationship suggests that negative energy plays a more critical role in high atomic number elements and larger cosmic structures, providing balance and ensuring the structural integrity of these systems.
Harmonic Resonance as a Source of Stability
Within the VFD framework, harmonic resonance is the mechanism through which stability is maintained across structures. Resonance occurs when a system’s vibrational modes align with its fundamental frequencies, leading to constructive interference that reinforces stability. This principle applies to atomic nuclei, where resonance stabilizes configurations with magic numbers, and to planetary orbits, where resonance patterns can prevent orbital decay.
To explore harmonic resonance in detail, we introduce the concept of harmonic expansions of the fundamental frequency:![]()
where:
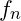 is the primary frequency at node nnn,
is the primary frequency at node nnn,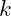 represents the harmonic level.
represents the harmonic level.
This harmonic expansion predicts that secondary stability points arise at integer multiples of the primary frequency, giving rise to a spectrum of stable configurations. For atomic structures, this translates to stable isotopes with distinct neutron-proton ratios, while in planetary systems, harmonic resonance nodes could explain orbital resonances observed in multi-body systems.
In the Vibrational Field Dynamics (VFD) framework, negative energy plays a key role as a stabilizing influence that counterbalances the positive forces within atomic and cosmic structures. This concept expands on the traditional view of forces, proposing that negative energy is a fundamental component that maintains equilibrium by balancing out the otherwise disruptive influences of positive energy forces.
Nature of Negative Energy in VFD
Negative energy, as introduced in VFD, isn’t simply the absence of energy; rather, it represents a counteracting influence that dissipates energy in a way that allows stable formations to persist. In this framework:
- Negative energy stabilizes systems by modulating or balancing positive forces that would otherwise cause instability, such as the repulsive forces between protons in an atomic nucleus.
- It decreases in influence with increasing frequency, meaning its stabilizing effect is more pronounced at lower frequencies (e.g., in larger cosmic structures) and less pronounced in higher-frequency, smaller atomic structures.
This duality is similar to how positive and negative charges balance each other out in electromagnetism. In VFD, negative energy provides a dampening force, working to maintain structural integrity across scales.
Mathematical Representation of Negative Energy
In the mathematical model of VFD, negative energy is expressed as a frequency-dependent function:![]()
where:
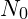 is a constant defining the base level of negative energy,
is a constant defining the base level of negative energy,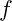 is the frequency associated with a specific stability node,
is the frequency associated with a specific stability node,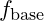 is the base frequency for the system (atomic or cosmic),
is the base frequency for the system (atomic or cosmic),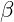 controls how strongly negative energy scales with frequency,
controls how strongly negative energy scales with frequency,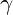 is a decay constant, determining how quickly negative energy influence diminishes at high frequencies.
is a decay constant, determining how quickly negative energy influence diminishes at high frequencies.
This function captures the inverse relationship between negative energy influence and frequency, as it shows that negative energy is most impactful at lower frequencies and gradually decreases with higher frequencies.
Role of Negative Energy in Atomic Stability
In atomic nuclei, the strong nuclear force binds protons and neutrons together, but this attractive force is not unlimited—it begins to weaken in the presence of large numbers of protons, especially in heavy elements. Negative energy in VFD functions as an additional stabilizer:
- It helps to counterbalance the repulsive forces among protons, particularly in larger nuclei where positive forces alone would destabilize the structure.
- By providing a stabilizing influence that counteracts positive forces, negative energy can extend stability to elements with higher atomic numbers, potentially explaining the existence of “magic numbers” (configurations of protons and neutrons that exhibit unusual stability).
This role of negative energy aligns with the concept of the “island of stability” for superheavy elements, suggesting that certain isotopic configurations can persist despite high proton counts, as long as negative energy provides adequate balance.
Role of Negative Energy in Cosmic Stability
In cosmic structures, negative energy provides balance against gravitational collapse in large systems, such as solar systems or galaxies:
- Balancing Gravitational Attraction: As gravitational forces pull celestial bodies together, negative energy creates a counteracting force that helps maintain stable orbits and prevents collapse.
- Frequency Scaling: Since cosmic structures operate at relatively lower frequencies compared to atomic systems, negative energy’s influence remains significant over large distances. This might help explain why planetary orbits and galaxy formations exhibit stability and resilience over long periods.
Negative Energy’s Modulating Effect and Resonance Nodes
Negative energy is also responsible for helping maintain resonance nodes by modulating energy distribution across harmonic frequencies:
- Resonance and Negative Energy: When a system resonates at a specific frequency, negative energy dampens any fluctuations that deviate from this resonance, reinforcing the stability of the node.
- Harmonic Expansion and Stability: Negative energy enables certain harmonic frequencies to become stable nodes, leading to configurations like magic numbers in atomic nuclei and resonant orbits in celestial systems. Without negative energy’s modulating effect, these stable points might be far more limited in number and persistence.
Predictive Power of Negative Energy in VFD
The concept of negative energy as a stabilizing force opens predictive possibilities:
- In Nuclear Physics: By modeling negative energy’s role in stabilizing high atomic numbers, VFD can predict potential isotopes or new elements that may exist within a range of stability supported by negative energy.
- In Astrophysics: The balance of gravitational and negative energy influences in cosmic structures could lead to predictions about the distribution and stability of celestial bodies within galaxies, contributing to a unified field model that connects nuclear and cosmic stability.
In VFD, negative energy is more than an abstract counterbalance; it is a dynamic stabilizing influence that enables both atomic and cosmic structures to maintain stability at specific frequency nodes. As structures scale up, negative energy becomes a larger factor, providing stability boundaries that would otherwise collapse under gravitational or nuclear forces alone. The role of negative energy within VFD not only helps to maintain stability across scales but also suggests that balanced, self-similar structures are a natural consequence of vibrational dynamics in a unified field. This foundational concept provides an alternative to traditional models and serves as a core component of VFD’s predictive power.
Mathematical Framework for Stability in Vibrational Field Dynamics
Frequency Scaling and Effective Forces in Atomic and Cosmic Stability
In the VFD framework, stability nodes arise from the balance between positive forces (such as gravitational or nuclear attraction) and negative energy’s stabilizing influence. To quantify this, we introduce frequency scaling as the primary determinant of stability. For each stability node, a base frequency is scaled according to the golden ratio, defining harmonic points where structures can exist in balanced configurations.
Frequency Scaling Using the Golden Ratio
Following the principles outlined in earlier, we define the fundamental frequency scaling equation as: ![]()
where:
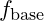 is the fundamental frequency that defines the initial resonance point in a given structure (e.g., an atomic nucleus or planetary orbit),
is the fundamental frequency that defines the initial resonance point in a given structure (e.g., an atomic nucleus or planetary orbit), is the golden ratio, approximately 1.618,
is the golden ratio, approximately 1.618,- nnn is the harmonic node number, an integer representing each subsequent stability point in the sequence.
This equation creates a series of frequencies that increase according to the golden ratio. These frequencies represent resonance nodes where balanced configurations are achievable. In atomic contexts, these nodes correlate with magic numbers that define stable nucleon arrangements, while in cosmic systems, they describe orbital resonances that prevent decay.
Effective Nuclear Force as a Frequency-Dependent Influence
Within the nucleus, stability is typically attributed to the strong nuclear force, which binds protons and neutrons together. In VFD, this force is considered an effective force that varies inversely with frequency. To model this, we introduce an effective nuclear influence, ![]()
where:
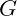 is a proportional constant representing the base nuclear attraction (analogous to gravitational or nuclear constants),
is a proportional constant representing the base nuclear attraction (analogous to gravitational or nuclear constants),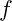 is the frequency at a given node,
is the frequency at a given node,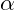 is a scaling exponent that dictates how the effective force scales with frequency.
is a scaling exponent that dictates how the effective force scales with frequency.
As frequency increases, the effective nuclear influence decreases, creating stability boundaries. This equation suggests that, at high frequencies, the attraction between nucleons lessens, potentially leading to instability in high-energy systems.
Negative Energy Influence and Stability Boundaries
Building on our discussion in earleir, negative energy provides a frequency-dependent stabilization that balances the positive forces within atomic and cosmic structures. Negative energy’s influence decreases with increasing frequency, which is particularly relevant in systems where high frequencies would otherwise destabilize structural configurations.
Negative Energy Influence Function
To capture the stabilizing effect of negative energy, we define a frequency-dependent function, N_{\text{eff}} = N_0 \cdot \left(\frac{f}{f_{\text{base}}}\right)^{\beta} \cdot e^{-\gamma f}
where:
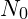 is a base constant representing the initial level of negative energy,
is a base constant representing the initial level of negative energy,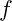 is the frequency at a particular stability node,
is the frequency at a particular stability node,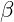 modulates the scaling effect of frequency on negative energy,
modulates the scaling effect of frequency on negative energy,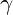 controls the exponential decay, determining how quickly negative energy diminishes with increasing frequency.
controls the exponential decay, determining how quickly negative energy diminishes with increasing frequency.
In this model:
- At lower frequencies,
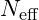 has a strong stabilizing effect, balancing the positive forces and allowing configurations like magic numbers in atomic nuclei to form.
has a strong stabilizing effect, balancing the positive forces and allowing configurations like magic numbers in atomic nuclei to form. - At higher frequencies, the influence of negative energy decreases, leading to stability boundaries where additional nucleons or orbital positions may become unsustainable.
This function provides an essential balancing term, enabling stability where otherwise high energy or repulsive forces would cause disruption.
Net Stability Function for Unified Stability Prediction
By combining the effective nuclear force and negative energy influence, we can create a net stability function that describes the balance of forces at any given frequency node. This function provides a unified measure of stability, applicable to both atomic and cosmic systems.
Net Stability Function
The net stability function, ![]()
Expanding ![]() and
and ![]() in terms of their frequency-dependent components, we obtain:
in terms of their frequency-dependent components, we obtain:![]()
where:
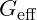 and
and 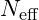 represent the positive and negative influences at a given frequency, respectively,
represent the positive and negative influences at a given frequency, respectively,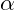 ,
, 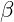 , and
, and 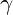 are scaling exponents that determine the relative influence of each component.
are scaling exponents that determine the relative influence of each component.
Interpretation of the Net Stability Function
- Stable Nodes: Stability is achieved at nodes where
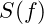 approaches zero, indicating that the positive and negative forces are in equilibrium. This balance suggests a natural resonance point, where a structure such as an atomic nucleus or a planetary orbit can exist stably without further disruption.
approaches zero, indicating that the positive and negative forces are in equilibrium. This balance suggests a natural resonance point, where a structure such as an atomic nucleus or a planetary orbit can exist stably without further disruption. - Instability Thresholds: As
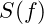 diverges from zero, the system approaches instability boundaries. For high atomic numbers or close-orbit planetary configurations,
diverges from zero, the system approaches instability boundaries. For high atomic numbers or close-orbit planetary configurations, 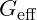 may weaken, or
may weaken, or 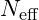 may decline, leading to configurations that are unstable.
may decline, leading to configurations that are unstable. - Predicted Nodes for Atomic and Cosmic Structures: By solving for fff when
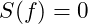 , we can predict resonance nodes that correspond to stable configurations. In atomic systems, these nodes align with magic numbers, while in cosmic systems, they may correspond to resonant orbital distances.
, we can predict resonance nodes that correspond to stable configurations. In atomic systems, these nodes align with magic numbers, while in cosmic systems, they may correspond to resonant orbital distances.
Implications for Predicting Stability Across Scales
This function provides a universal tool for predicting stability across both atomic and cosmic systems, allowing for:
- Prediction of Stable Isotopes: For atomic nuclei, we can calculate frequency nodes where the proton-neutron ratio aligns with stability nodes, indicating likely configurations for stable or metastable isotopes.
- Prediction of Planetary Orbital Resonances: In cosmic structures, the same function can predict distances or orbital velocities where negative energy stabilizes gravitational forces, creating balanced orbits or resonance patterns in multi-body systems.
Harmonic Expansion and Stability Variations
Beyond primary resonance nodes, harmonic expansions provide insight into secondary stability points. These harmonic frequencies allow for sub-nodes where stability is partially reinforced, yielding metastable configurations or isotopic variants within atomic structures and sub-orbital resonances in planetary systems.
Harmonic Expansion of Frequency Nodes
The harmonic expansion for each primary node is given by:![]()
where:
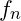 is the primary frequency at the nnn-th node,
is the primary frequency at the nnn-th node,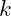 is an integer representing the harmonic level.
is an integer representing the harmonic level.
Harmonic Stability Function
Using the net stability function S(f), we can assess the stability at harmonic frequencies: ![]()
Harmonic stability points may indicate metastable states, where structures are temporarily stable but prone to decay over time. In atomic contexts, these points align with isotopic variants of known elements, while in cosmic systems, they correspond to secondary orbital positions.
In the Vibrational Field Dynamics (VFD) framework, harmonic resonance plays a crucial role in establishing and reinforcing stability nodes across atomic and cosmic structures. Harmonic resonance provides a multi-layered structure where frequencies resonate not only at primary nodes but also at integer multiples of these nodes, resulting in a pattern of stability and reinforcing certain configurations over others. This effect underpins the formation of stable isotopes in atoms and resonant orbits in planetary systems, linking different scales through universal principles.
Concept of Harmonic Resonance in VFD
Harmonic resonance refers to the phenomenon where a frequency at one stability node is amplified or reinforced by vibrations at higher, related frequencies—multiples of the primary frequency. This resonance effect is central to VFD, as it suggests that stability is not just achieved at single, isolated frequencies but across a spectrum of harmonics, creating a web of stability points that are interdependent and self-reinforcing.
In simpler terms:
- Each primary frequency node has a set of harmonic frequencies that resonate with it, amplifying its stability.
- The resonance effect leads to configurations where elements like atoms or celestial bodies are more likely to form stable arrangements.
Mathematical Formulation of Harmonic Frequencies
In VFD, each primary frequency node ![]() can generate harmonic nodes at integer multiples, denoted as f_{n,k}, where
can generate harmonic nodes at integer multiples, denoted as f_{n,k}, where ![]() is the harmonic level:
is the harmonic level: ![]()
where:
-
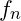 is the primary frequency at node nnn,
is the primary frequency at node nnn, 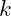 represents the harmonic number (e.g.,
represents the harmonic number (e.g., 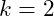 for the first harmonic,
for the first harmonic, 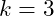 for the second harmonic, etc.).
for the second harmonic, etc.).
These harmonic nodes create secondary stability points in systems where additional layers of resonance reinforce stability. This pattern means that if fnf_nfn is a stable primary node, then the harmonics of ![]() (like
(like ![]() ,
, ![]() , etc.) will also exhibit stability, but with potentially diminishing influence as
, etc.) will also exhibit stability, but with potentially diminishing influence as ![]() increases.
increases.
Implications of Harmonic Resonance for Atomic Stability
In atomic systems, harmonic resonance contributes to the stability of isotopes and magic numbers:
- Isotopic Stability: Harmonic resonance provides additional stability for nuclei with specific neutron-proton ratios that align with harmonic frequencies. This effect explains why certain isotopes are more stable than others, even when they have similar compositions. Magic numbers of protons and neutrons (e.g., 2, 8, 20, 28, etc.) correspond to primary nodes, with stable isotopes appearing at harmonics of these numbers.
- Metastable Isotopes: In some cases, harmonic resonance can create metastable states—configurations that are not fully stable but exist with some stability due to harmonic reinforcement. These isotopes may decay over time but persist longer than non-resonant configurations.
For example, an isotope at a primary frequency ![]() may exhibit long-term stability, while an isotope at a harmonic frequency
may exhibit long-term stability, while an isotope at a harmonic frequency ![]() (the second harmonic) may be metastable, meaning it has a slower decay rate due to partial stability reinforcement.
(the second harmonic) may be metastable, meaning it has a slower decay rate due to partial stability reinforcement.
Implications of Harmonic Resonance for Cosmic Stability
In cosmic systems, harmonic resonance has similar effects on planetary orbits and celestial resonances:
- Orbital Resonances: Harmonic nodes in planetary systems can create resonant orbits where celestial bodies (such as planets or moons) maintain stable paths due to harmonic alignment. For instance, orbital resonances (such as the 2:1 resonance between Jupiter’s moons) occur when the orbital periods of two bodies align in integer ratios, effectively synchronizing their gravitational influence and reinforcing their orbital paths.
- Resonance Chains: In some planetary systems, a chain of planets or moons may form where each body’s orbit resonates harmonically with its neighbors. This creates a stabilizing feedback loop where each body’s orbit is reinforced by the harmonic resonance with its adjacent bodies, leading to configurations that are highly stable over time.
In these systems, harmonic resonance provides an explanation for the spacing of planetary orbits and why certain orbits are more stable than others.
Harmonic Stability Function in VFD
To quantify harmonic resonance within the VFD framework, we use the harmonic stability function, which calculates stability at each harmonic node ![]() by applying the net stability function at these points:
by applying the net stability function at these points:![]()
where:
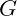 represents the effective nuclear or gravitational influence,
represents the effective nuclear or gravitational influence,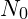 ,
, 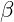 , and
, and 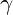 describe the negative energy influence as detailed earlier,
describe the negative energy influence as detailed earlier,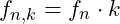 is the harmonic frequency,
is the harmonic frequency,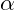 adjusts the scaling of the effective force.
adjusts the scaling of the effective force.
In this formulation:
- Stable Harmonic Nodes: A harmonic node
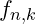 is stable when
is stable when 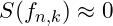 , suggesting an equilibrium between positive and negative forces.
, suggesting an equilibrium between positive and negative forces. - Metastable Harmonic Nodes: Nodes where
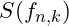 ) is near but not equal to zero indicate partial stability, leading to metastable configurations.
) is near but not equal to zero indicate partial stability, leading to metastable configurations.
This function allows us to calculate the stability or metastability of different harmonic nodes within atomic and cosmic systems.
Practical Applications of Harmonic Resonance in Predictive Modeling
Harmonic resonance enables predictive modeling within both atomic and cosmic systems by allowing us to:
- Predict Isotopic Variants: By applying the harmonic stability function to primary frequency nodes, we can estimate which isotopic configurations are likely to be stable or metastable, particularly for superheavy elements.
- Predict Resonant Orbits: In planetary systems, the harmonic stability function can help identify preferred orbital distances or configurations, as seen in Laplace resonances or mean-motion resonances among planets or moons.
Summary of Harmonic Resonance in VFD
In the VFD model, harmonic resonance provides a multilayered stability framework where primary stability nodes are reinforced by harmonics. This concept of resonance across multiple scales helps explain phenomena as diverse as:
- Magic numbers and isotopic stability in nuclear physics,
- Orbital resonances and planetary spacing in astrophysics.
By expanding on the primary frequency nodes with harmonic resonance, VFD not only offers a predictive tool but also suggests that stability across scales is an emergent property of resonance patterns—a self-reinforcing process that leads to structural configurations observed across the natural world.
Predictive Applications of Vibrational Field Dynamics in Atomic and Cosmic Systems
Predicting Elemental Stability and Isotopic Variants
One of the primary applications of VFD is the ability to predict stable configurations in atomic nuclei, particularly among superheavy elements and isotopic variants. By applying frequency scaling, harmonic resonance, and negative energy influence, VFD allows us to calculate stability nodes for various proton-neutron ratios, giving insights into the stability of both naturally occurring and synthetic isotopes.
Stability Prediction for Superheavy Elements
The net stability function derived earlier offers a pathway to model potential stability for superheavy elements. These elements, which have large proton and neutron counts, are typically prone to rapid decay due to strong repulsive forces among protons. However, VFD suggests that specific configurations—where harmonic resonance and negative energy provide stability—may enable these elements to exist longer than traditional models predict.
To apply the net stability function:
- Calculate the Primary Frequency Nodes: Using the golden ratio-based frequency scaling, we calculate the primary resonance frequency for a given element’s proton and neutron count. For instance, if we aim to predict the stability of a hypothetical element with 119 protons and 175 neutrons, we apply:
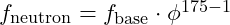
- Apply the Net Stability Function: Calculate the stability at these nodes using:
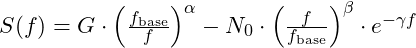
- Assess Stability: If
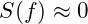 , the element is predicted to be stable or metastable. For elements with high atomic numbers, partial stability can indicate configurations that may not decay instantaneously, potentially forming new isotopes within the “island of stability.”
, the element is predicted to be stable or metastable. For elements with high atomic numbers, partial stability can indicate configurations that may not decay instantaneously, potentially forming new isotopes within the “island of stability.”
This process allows us to identify which proton-neutron configurations are likely to result in more stable superheavy elements, providing valuable insights for experimental physicists working on element synthesis.
Isotopic Variants and Harmonic Resonance
In addition to predicting new elements, VFD’s harmonic resonance model helps identify isotopic variants within known elements. By calculating harmonic expansions for primary frequency nodes, we can determine which isotopes are likely to be stable or metastable based on their alignment with harmonic nodes.
- Calculate Harmonic Frequencies: For a primary stability node, calculate the harmonic frequencies:
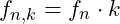
- Evaluate Harmonic Stability: Apply the stability function at these harmonic nodes:
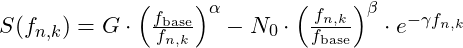
This harmonic approach suggests that certain isotopes, while not entirely stable, may exist in metastable states, particularly if they align with harmonic nodes that partially reinforce stability. For example, elements such as Uranium and Thorium have multiple isotopes due to these harmonic influences, with certain isotopes exhibiting half-lives long enough for practical study.
Implications for Experimental Verification
The ability of VFD to predict stability in superheavy elements and isotopes offers a promising framework for nuclear experimentation. By targeting specific proton-neutron configurations that align with VFD stability predictions, experimental physicists can focus on feasible synthesis pathways for new elements and isotopes, minimizing trial-and-error experimentation. This model may also aid in identifying isotopes with longer half-lives or stability-enhancing harmonic nodes, improving our understanding of nuclear stability.
Predicting Orbital Resonances and Planetary Stability
Beyond atomic structures, VFD’s principles of frequency scaling and harmonic resonance extend naturally to cosmic structures, where they explain the stability of planetary orbits and orbital resonances among celestial bodies.
Stability Prediction in Planetary Orbits
In planetary systems, harmonic resonance can create stable orbital configurations, where gravitational interactions reinforce specific orbits. VFD models this using the same principles applied to atomic stability, with gravitational forces analogous to nuclear forces and planetary distances scaling according to harmonic nodes.
To predict stable orbital configurations:
- Calculate Orbital Frequency Nodes: For each planet, calculate an orbital frequency using a fundamental base frequency and harmonic scaling:
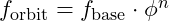 could be the orbital frequency of an inner planet or the fundamental resonance of the central star.
could be the orbital frequency of an inner planet or the fundamental resonance of the central star. - Evaluate Stability Across Harmonic Nodes: Apply the net stability function to assess each orbit’s stability, taking into account gravitational influences and distance scaling:
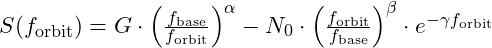
This function can highlight preferred distances where stable orbits are likely to form, providing insight into the spacing between planets in a solar system.
Resonant Chains and Mean-Motion Resonances
Harmonic resonance also explains mean-motion resonances and resonant chains, where multiple planets or moons orbit in synchronized patterns. In these cases, the orbits of neighboring celestial bodies align at specific harmonic ratios (such as 2:1 or 3:2), reinforcing each other’s stability.
- Calculate Resonant Ratios: For a resonant chain, determine the harmonic ratio between orbits:
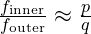 where
where 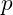 and
and 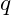 are integers representing the resonance ratio (e.g., a 2:1 resonance).
are integers representing the resonance ratio (e.g., a 2:1 resonance). - Determine Stability at Harmonic Ratios: Evaluate the stability function at these resonant ratios, which aligns with the harmonic nodes identified in VFD. If
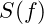 is near zero, the configuration is likely to be stable, with each body’s orbit resonating harmonically with its neighbors.
is near zero, the configuration is likely to be stable, with each body’s orbit resonating harmonically with its neighbors.
Applications in Observational Astronomy
By predicting resonant orbits and planetary spacing, VFD offers practical applications in observational astronomy. These predictions can guide the search for exoplanetary systems, where orbital resonances might suggest the presence of undiscovered planets or moons. Additionally, VFD’s principles provide a framework for analyzing multi-planet systems where harmonic resonance stabilizes complex orbital arrangements, such as those found in Laplace resonances in the outer solar system.
Summary of Predictive Applications
The predictive power of VFD lies in its ability to unify the principles of frequency scaling, harmonic resonance, and negative energy across both atomic and cosmic scales. In nuclear physics, VFD allows for the identification of stable and metastable isotopes, guiding element synthesis and improving our understanding of nuclear stability boundaries. In astrophysics, VFD explains planetary resonances and orbital spacing, offering a predictive model for observing and understanding multi-body systems.
By bridging these scales, VFD not only provides a framework for understanding stability but also opens possibilities for practical applications in experimental physics and astronomy. The next section will delve into the theoretical and experimental implications of VFD, discussing how its principles could be tested and validated through current and future research initiatives.
Theoretical and Experimental Implications of Vibrational Field Dynamics
Experimental Pathways in Nuclear Physics
VFD’s approach to elemental stability and harmonic resonance opens new avenues for experimentation in nuclear physics. By leveraging the concepts of frequency scaling and negative energy influence, this framework provides specific predictions about the stability of superheavy elements and isotopes. This section discusses the experimental pathways for testing these predictions in controlled laboratory environments, specifically through particle accelerators and isotope synthesis experiments.
Testing Stability Predictions in Superheavy Elements
The VFD framework predicts that superheavy elements can achieve stability at specific resonance nodes, aligning with frequency scaling based on the golden ratio. To experimentally verify this, particle accelerators can be used to synthesize elements at these predicted stability points. Here’s how this might be approached:
- Element Synthesis Based on Stability Nodes: Using particle accelerators, researchers could target specific proton-neutron configurations that align with VFD’s predicted stability nodes. For instance, an experiment could be designed to synthesize elements with proton-neutron ratios near harmonic stability nodes predicted by VFD’s net stability function.
- Longer Half-Life as an Indicator: One of the primary indicators of stability in superheavy elements is an extended half-life. Elements synthesized at VFD-predicted stability nodes should theoretically exhibit longer half-lives than those synthesized at arbitrary configurations. Researchers can measure the decay rates of these synthesized elements to compare with the predictions of VFD.
- Comparing Experimental Data to VFD Calculations: By calculating expected stability using the net stability function for various synthesized elements, researchers can compare observed stability with theoretical predictions. If elements synthesized at VFD stability nodes display enhanced stability, this would provide strong support for VFD’s resonance-based model.
Harmonic Expansion for Isotopic Stability
Another promising avenue for experimentation involves studying isotopic stability in known elements, particularly those with multiple stable isotopes. VFD suggests that isotopes aligned with harmonic nodes will exhibit longer half-lives, potentially allowing the identification of metastable configurations in existing elements.
- Creating and Testing Metastable Isotopes: By targeting isotopes at predicted harmonic frequencies, researchers can test whether these isotopes exhibit partial stability as VFD predicts. This can be done by creating isotopic variants through particle accelerators and analyzing their decay behavior.
- Spectroscopy and Isotope Detection: Spectroscopic analysis can help identify specific isotopes that resonate at harmonic nodes. Using ultra-sensitive spectrometers, researchers can detect isotopes that exhibit resonant frequencies aligning with VFD’s harmonic expansions, providing further support for VFD’s resonance-based model.
Implications for Nuclear Stability Research
If VFD’s predictions about stable and metastable isotopes prove accurate, this could lead to a revised understanding of nuclear stability boundaries, especially among superheavy elements. This framework could potentially identify new elements within the “island of stability”, expanding our understanding of the periodic table and guiding future experiments in nuclear physics.
Observational Pathways in Astrophysics
In astrophysics, VFD’s principles of frequency scaling, harmonic resonance, and negative energy provide a framework for understanding planetary resonances and orbital stability. Observational astronomy offers a unique testing ground for these principles, as many VFD predictions about cosmic structures can be verified through high-resolution imaging, spectroscopy, and data analysis of exoplanetary systems.
Detecting Orbital Resonances in Exoplanetary Systems
One of VFD’s key predictions is that planetary orbits in stable systems will often exhibit harmonic resonance patterns, with orbital periods aligning at integer ratios. Observing these patterns in exoplanetary systems could provide strong evidence for VFD’s resonance-based model of stability.
- Targeted Exoplanet Observations: Using telescopes capable of detecting exoplanet transits, astronomers could focus on multi-planet systems to identify orbital ratios that align with harmonic resonances predicted by VFD. Systems exhibiting mean-motion resonances or Laplace resonances would be of particular interest.
- Data Analysis for Harmonic Ratios: By analyzing exoplanetary data, astronomers can determine whether the orbits of planets in these systems align with harmonic ratios, as VFD predicts. Observing resonances such as 2:1 or 3:2 between orbital periods would support the idea that harmonic nodes contribute to cosmic stability.
- Comparing Observational Data to VFD Predictions: By applying VFD’s stability function to calculate preferred orbital distances or resonance ratios, astronomers can compare observed exoplanetary configurations with theoretical predictions. Systems that align with VFD-predicted resonances would provide empirical support for VFD’s harmonic resonance model.
Analyzing Resonant Chains and Planetary Spacing
VFD suggests that resonant chains and specific planetary spacing patterns arise from harmonic resonance, where the spacing between planets follows predictable ratios. This concept can be tested by analyzing planetary spacing in multi-planet systems.
- Studying Resonant Chains in Known Planetary Systems: Planetary systems with resonant chains, such as the TRAPPIST-1 system, provide an excellent test case for VFD’s harmonic resonance predictions. By analyzing the resonant chain and comparing it to harmonic expansions, astronomers can verify if VFD’s frequency-based model accurately predicts planetary spacing.
- Mapping Planetary Distances: Using high-resolution data on planetary distances, astronomers can map the spacing of planets within multi-planet systems and identify patterns of harmonic spacing. Observing alignment with VFD-predicted resonance nodes would strengthen the case for VFD as a framework for cosmic stability.
- Implications for Planet Formation Theories: If VFD’s predictions align with observed planetary spacing, this could challenge traditional models of planet formation. The idea that harmonic resonance governs planetary spacing would imply a frequency-based organization of matter at cosmic scales, suggesting that resonant patterns play a fundamental role in the formation and stability of planetary systems.
Implications for Unified Physics and Cross-Disciplinary Research
The principles of VFD provide a novel framework for understanding stability across different scales, bridging the gap between nuclear physics and astrophysics. This section discusses the broader implications of VFD, particularly its potential as a unified theory of stability that applies to both atomic and cosmic structures.
A Unified Framework for Stability
VFD’s reliance on frequency scaling, harmonic resonance, and negative energy offers a unified approach to stability, suggesting that vibrational resonance underpins structural integrity across scales. This unifying perspective has implications for:
- Nuclear and Atomic Physics: VFD offers a pathway to identify stability nodes in nuclear structures, providing insights into why certain elements and isotopes exhibit long-term stability.
- Astrophysics and Cosmology: The same principles that explain atomic stability are applied to cosmic scales, suggesting that planetary orbits and galactic structures are governed by frequency-based resonance patterns.
This unified framework could inspire cross-disciplinary research, encouraging collaboration between nuclear physicists and astrophysicists in studying resonance-based stability.
Implications for Experimental Physics
VFD’s predictions offer several potential tests across experimental physics. For example:
- Spectroscopy and Particle Acceleration: Testing VFD’s predictions about nuclear stability and isotopic variants would enhance our understanding of superheavy elements and potentially reveal new stability nodes on the periodic table.
- Resonance Experiments: Laboratory experiments could investigate whether the principles of harmonic resonance can be observed in smaller-scale systems, such as molecular or crystalline structures, to further validate VFD’s frequency-based approach.
Observational Challenges and Opportunities
Implementing VFD in observational astronomy presents unique challenges but also offers new opportunities. The need for precise measurements in multi-planet systems and detailed isotope analysis in nuclear physics highlights the importance of advanced technology. Potential observational techniques include:
- High-Resolution Telescopes: Space-based observatories with precise exoplanet detection capabilities could verify VFD predictions about orbital resonance.
- Spectroscopic Advances: Ultra-sensitive spectrometers could be used to detect harmonic frequencies in nuclear or molecular structures, providing experimental data that aligns with VFD’s theoretical predictions.
Summary of Experimental and Observational Pathways
VFD provides a framework that is ripe for experimental and observational testing, with applications ranging from superheavy element synthesis to planetary orbit analysis. By leveraging existing technologies and developing new approaches, physicists and astronomers can explore whether VFD’s predictions hold across different physical domains. This research could ultimately confirm VFD as a unified field theory of stability, linking the behavior of atomic and cosmic systems through frequency-based resonance patterns.
Theoretical Expansion and Future Applications of Vibrational Field Dynamics
Theoretical Expansion: Toward a Unified Frequency-Based Model
The principles of VFD—frequency scaling, harmonic resonance, and negative energy influence—suggest that vibrational patterns may be fundamental to understanding stability across vastly different scales. This section considers how these principles could be extended into a unified field theory, where atomic, molecular, planetary, and even galactic structures are described through a shared vibrational framework.
Vibrational Patterns as Fundamental Organizational Structures
In VFD, stability is achieved through resonant frequency nodes that align with predictable harmonic ratios. This vibrational framework could imply that all physical structures are simply manifestations of vibrational states within a single field. In this view:
- Quantum Particles as Vibrational Modes: Subatomic particles, such as electrons and quarks, may represent distinct frequency modes within a field, each stabilized by harmonic resonance.
- Molecular Bonds as Resonant Interactions: Molecular structures could be viewed as stable vibrational patterns, where atomic bonds form at resonant nodes, much like stable orbits in planetary systems.
This approach introduces the possibility that vibrational resonance isn’t just a feature of stability but the foundation of structural formation in the universe, suggesting a profound unity across physical systems.
Extending VFD to Quantum Mechanics and Relativity
A major goal in physics is the unification of quantum mechanics and relativity, two fields traditionally governed by separate mathematical frameworks. VFD could serve as a bridge between these domains:
- Quantum Mechanics and Frequency Nodes: In quantum mechanics, particles exhibit wave-particle duality, where each particle can be described by a wave function. VFD posits that these wave functions may arise as frequency nodes within a unified vibrational field, allowing particles to exhibit stability through resonance.
- Relativity and Cosmic Scale Resonance: In the context of relativity, VFD suggests that gravitational effects are also influenced by harmonic resonance patterns at cosmic scales. Frequency scaling could potentially modify our understanding of space-time curvature, offering a frequency-based perspective on gravitational interactions.
VFD bridges quantum mechanics and relativity through its frequency-based model, this implies a new unified theory of stability that applies across scales, providing a consistent framework for understanding both microscopic and macroscopic structures.
Future Applications of VFD Across Disciplines
The predictive power of VFD offers potential applications in fields beyond nuclear and astrophysics, particularly in molecular chemistry, materials science, and biophysics. The principles of harmonic resonance and stability nodes may provide new ways to design stable structures, understand material properties, and even explore biological resonance.
Applications in Molecular Chemistry
In molecular chemistry, the formation and stability of bonds can be influenced by vibrational resonance. VFD’s principles could provide a framework for understanding why certain molecular structures are more stable than others based on resonance patterns.
- Predicting Stable Molecular Structures: VFD’s harmonic expansion could help predict stable molecular configurations by identifying resonant bonding patterns between atoms. Molecules with configurations that align with resonance nodes may exhibit enhanced stability.
- Catalysis and Reaction Pathways: Catalytic reactions often depend on precise energy states for chemical bonds to form or break. VFD could provide insights into optimal vibrational states for catalysis, enabling more efficient chemical processes by aligning reaction pathways with resonant nodes.
Applications in Materials Science
Materials science seeks to understand and manipulate the properties of materials at the atomic level to create structures with desired characteristics. VFD could aid in the design of stable, resilient materials through resonance-based principles.
- Resonant Stability in Crystalline Structures: Crystals form in specific patterns due to stable atomic arrangements. VFD’s resonance nodes could help predict the most stable crystalline configurations, potentially leading to stronger and more resilient materials.
- Vibrational Analysis for Material Strength: By understanding how harmonic resonance affects stability, VFD could help materials scientists identify frequency nodes that correspond to maximum material strength. This insight may guide the development of materials that are less prone to cracking, wear, and deformation under stress.
Applications in Biophysics and Cellular Resonance
Biophysics is increasingly focused on how vibrational frequencies within cellular structures contribute to biological function. VFD could provide a framework for studying biological resonance and its role in cellular stability.
- Protein Folding and Stability: Protein folding is influenced by molecular vibrations, which affect how proteins stabilize into functional shapes. VFD’s resonance model could help predict optimal folding configurations based on resonance nodes, improving our understanding of protein stability.
- Cellular Communication through Vibrational States: Some theories suggest that cells communicate through vibrational signals. VFD could offer a framework for studying frequency-based cellular communication, potentially uncovering new methods for influencing biological processes through resonance.
Future Directions in VFD Research
To advance the theory and its applications, further research is needed across both theoretical and experimental domains. This section outlines some key research directions that could help validate and expand VFD as a comprehensive model of stability.
Experimental Verification of Resonance Nodes
While the predictive power of VFD is promising, its principles must be empirically validated. Key experiments include:
- Resonant Harmonic Detection in Atomic and Molecular Systems: Developing experiments that can detect harmonic resonance at specific frequency nodes within atomic and molecular structures. Precision spectroscopy and particle accelerators may be essential tools for these experiments.
- Observation of Cosmic Resonance Nodes: Observational studies of exoplanetary systems to verify orbital resonance predictions made by VFD. With advancements in telescope technology, astronomers could detect resonance patterns that align with VFD’s harmonic model.
Mathematical Expansion for Greater Predictive Precision
Further mathematical refinement is essential for enhancing VFD’s predictive power. This may include:
- Refining the Net Stability Function: Expanding the stability function to include higher-order terms that account for more complex interactions in large atomic nuclei or multi-body systems.
- Developing Computational Models: Leveraging machine learning and computational simulations to model VFD’s predictions across large datasets. This would allow researchers to validate VFD’s principles over a wide range of atomic, molecular, and cosmic structures.
Integration with Existing Theories
VFD has the potential to integrate with other theoretical frameworks, potentially offering new insights into existing phenomena.
- Integration with Quantum Field Theory (QFT): Exploring how VFD’s resonance nodes align with quantum field fluctuations could bridge VFD with QFT, offering a unified view of particle interactions as vibrational phenomena.
- Compatibility with General Relativity: Investigating how VFD’s harmonic scaling influences gravitational interactions could reveal connections between VFD and general relativity, particularly in explaining stable cosmic structures.
Potential Paradigm Shift: Toward a Frequency-Based View of Reality
If validated, VFD could represent a paradigm shift in physics, offering a unified theory that describes stability through frequency and resonance rather than isolated forces. This view could fundamentally reshape our understanding of matter and energy by emphasizing that vibrational resonance patterns underlie all physical structures. Potential implications include:
- Redefining Fundamental Forces: VFD suggests that fundamental forces (gravitational, nuclear, and electromagnetic) may all emerge from underlying vibrational dynamics, challenging the notion of separate fundamental interactions.
- A New Interpretation of Mass and Energy: VFD proposes that mass and energy are not independent properties but rather emergent properties of resonance within a unified vibrational field, offering a potential path toward a unified field theory.
Summary of Future Applications and Directions
VFD offers a versatile and transformative framework that extends far beyond atomic stability or cosmic structures, potentially impacting fields as diverse as materials science, molecular chemistry, and biophysics. Through continued experimentation, mathematical refinement, and interdisciplinary collaboration, VFD could become a cornerstone theory, redefining our approach to understanding physical stability and structural formation across the natural world.
Synthesis, Implications, and Roadmap for Future Research
Synthesis of VFD’s Core Principles
Vibrational Field Dynamics (VFD) represents a bold new framework for understanding stability across scales. Throughout this paper, we have introduced and developed a theory where stability in both atomic and cosmic structures is governed by frequency-based interactions and harmonic resonance within a vibrational field. Here we summarize the core principles that make VFD a potentially unifying theory for physics:
Frequency Scaling and Harmonic Nodes
At the heart of VFD lies the idea that stability arises from frequency scaling, where structures align with specific resonance nodes based on integer multiples of a base frequency. The scaling factor, often linked to the golden ratio, provides a consistent model for predicting stability points across both atomic and cosmic systems:
- Atomic Scale: In nuclear physics, harmonic resonance explains why certain proton-neutron configurations, especially those matching “magic numbers,” exhibit enhanced stability.
- Cosmic Scale: In astrophysics, frequency-based resonance nodes align with orbital distances, explaining why planetary systems often display harmonic resonances and why certain orbital arrangements are more stable than others.
Negative Energy as a Stabilizing Influence
The concept of negative energy in VFD serves as a counteracting force that balances positive forces such as nuclear attraction and gravitational pull. Negative energy diminishes with increasing frequency, stabilizing configurations at lower frequencies:
- Atomic Stability: In atomic nuclei, negative energy balances the repulsive forces between protons, contributing to the stability of high atomic number elements.
- Cosmic Stability: On cosmic scales, negative energy helps to counterbalance gravitational forces, maintaining stable orbits and preventing collapse, especially in multi-body systems like planetary and stellar clusters.
Harmonic Resonance and Metastable States
Harmonic resonance expands VFD’s framework by predicting secondary stability nodes at harmonic frequencies of primary resonance points. These nodes suggest that stability is a layered phenomenon, where certain configurations are stable, while others exhibit partial stability or metastability:
- In Nuclear Physics: Harmonic nodes correspond to isotopic variants, indicating that specific isotopes exhibit metastable properties based on their alignment with these nodes.
- In Astrophysics: Harmonic resonance predicts the occurrence of orbital resonances, where celestial bodies maintain stable orbits by aligning with the harmonic frequencies of their neighbors.
Implications of VFD as a Unified Theory
If validated, VFD’s principles would represent a paradigm shift in physics, suggesting that vibrational resonance is the fundamental driver of stability and structure across scales. This has significant implications for both our theoretical understanding and practical applications:
Redefining Fundamental Forces
VFD challenges the traditional notion of separate forces (gravitational, electromagnetic, nuclear) by proposing that these forces emerge from frequency-based interactions within a unified field:
- Gravity and Negative Energy: Gravitational interactions in VFD are counterbalanced by negative energy, implying that gravitational stability arises from resonant nodes rather than purely attractive forces.
- Electromagnetic and Nuclear Forces: In VFD, nuclear and electromagnetic forces could be reframed as harmonic interactions within a vibrational field, rather than independent phenomena.
A New Perspective on Mass and Energy
In VFD, mass and energy are not inherent properties but emerge from the resonant stability of vibrational patterns within the field. This perspective aligns with the concept that mass-energy equivalence is a product of resonance within the vibrational field, potentially leading to new insights into the relationship between mass, energy, and frequency.
Practical Applications in Technology and Material Science
The principles of VFD could lead to transformative advancements across fields:
- Materials Science: By identifying harmonic stability points, VFD could guide the design of super-strong or resilient materials that utilize resonance for enhanced durability.
- Quantum Computing and Information Technology: VFD’s principles could inform the development of frequency-based quantum circuits, where stability is achieved through harmonic resonance, potentially offering greater coherence in quantum states.
Roadmap for Experimental and Theoretical Validation
To move VFD from a theoretical model to a validated framework, a systematic program of experimental and theoretical research is essential. Below are proposed directions for further research.
Experimental Verification of Harmonic Resonance
Testing harmonic resonance predictions in both atomic and cosmic systems is critical to validating VFD:
- Atomic Scale: Precision spectroscopy and particle accelerators can be used to synthesize isotopes at VFD-predicted stability nodes, testing whether they exhibit longer half-lives than random configurations.
- Cosmic Scale: Observational studies of multi-planet exoplanetary systems could confirm harmonic orbital resonances, especially if systems display resonant chains or mean-motion resonances predicted by VFD.
Refinement of Mathematical Models
The mathematical framework of VFD must be refined to increase its predictive precision, particularly in complex multi-body systems:
- Stability Function Optimization: Expanding the net stability function with higher-order terms can allow for better predictive power in complex atomic nuclei or cosmic structures.
- Computational Simulations: Leveraging machine learning and simulations could enable a thorough exploration of stability nodes across scales, allowing researchers to test VFD’s predictions on a broader scale.
Integration with Quantum and Relativistic Physics
VFD’s principles should be explored in the context of quantum mechanics and relativity to test its potential as a unified field theory:
- Quantum Harmonic Resonance: Future studies could explore how VFD’s harmonic nodes align with quantum wave functions, potentially bridging the gap between VFD and quantum field theory.
- Cosmic Resonance and Spacetime Curvature: The impact of harmonic resonance on spacetime curvature, particularly in high-gravity environments, could reveal connections between VFD and general relativity, opening pathways for a unified theory of gravity.
Conclusion: Toward a Frequency-Based Understanding of Reality
The potential of VFD to unify stability across scales—from atomic nuclei to planetary systems—offers a fundamentally new perspective on physics. By framing stability as a function of frequency scaling, harmonic resonance, and negative energy, VFD challenges existing theories while providing a framework that is both predictive and testable.
As we move forward, the validation of VFD’s principles could reshape our understanding of the fundamental forces, redefine the concepts of mass and energy, and inspire new technologies grounded in vibrational resonance. This shift to a frequency-based model of reality has the potential to unify the seemingly disparate realms of quantum mechanics, relativity, and cosmic structure, ushering in a new era of physics rooted in the resonant patterns that underlie the universe itself.


