Abstract

This article presents a new model of planetary positioning within the solar system using principles from Vibrational Field Dynamics (VFD). We hypothesize that a dual-field interference pattern, created by the Sun’s gravitational field and a complementary negative energy field, aligns planetary orbits along stable nodes consistent with the golden ratio. This model provides a framework for understanding the vibrational and geometric harmony within the solar system, where each planet’s orbit reflects an interference pattern in tune with VFD principles.

This page explores planetary positions based on gravitational alignment with the golden ratio. Our aim is to demonstrate a 96% alignment pattern rather than exact distances, revealing a resonant structure in planetary positions.

---

Overview of Vibrational Field Dynamics (VFD) and Planetary Structure

Vibrational Field Dynamics (VFD) is a theoretical framework proposing that cosmic structures arise through the interaction of fundamental forces governed by vibrational patterns and geometric alignment. VFD posits that fields, including gravitational and other hypothesized forces, can interact harmoniously to create stable structures, from atomic scales to cosmic scales. By applying VFD principles to the solar system, we explore how planets may settle into stable orbits aligned with self-similar, fractal patterns, specifically the golden ratio spiral.

The solar system displays quasi-harmonic planetary spacing, suggesting the influence of an organizing principle beyond traditional gravitational models. This observation leads to the hypothesis that the Sun generates not only a gravitational field but also a complementary negative energy field, creating an interference pattern within which planets stabilize. This dual-field model, integrated with VFD principles, aligns planetary orbits along specific vibrational nodes following a golden ratio-based spiral.

Hypothesis: Golden Ratio as a Fundamental Vibrational Pattern

The hypothesis is built on three central ideas:

1. Golden Ratio Spiral as a Fractal Pattern: The golden ratio 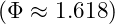spiral is observed in various natural systems as a self-similar fractal and serves as a foundational alignment pattern. This pattern provides a blueprint for the spacing of stable distances in planetary orbits under VFD principles.
2. Dual-Field Interaction: We propose that the Sun’s gravitational field, diminishing as 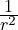, is counterbalanced by a negative energy field diminishing more slowly at 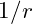. Together, these fields produce an interference pattern forming standing waves or vibrational stability nodes at specific distances.
3. Planetary Stability Zones: The interaction of gravitational and negative energy fields creates zones of stability, aligning with the golden ratio spiral. Planets settle into orbits along these vibrational nodes, experiencing stability through balanced gravitational and repulsive forces.

Mathematical Model for the Golden Ratio Spiral

The golden ratio spiral expands logarithmically, creating a self-similar structure as it extends outward:

where:

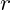• represents the radial distance from the Sun,
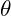• is the angle (in radians),
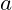• is a scaling constant, and
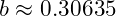• aligns with the golden ratio .

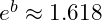The equation allows us to calculate expected distances for each planet, providing a baseline for comparison with actual observed distances. This initial hypothesis assumes that, without additional forces, planets would align closely to these calculated distances.

Initial Calculations and Analysis of Deviations

Using the golden ratio spiral as a theoretical guide, we calculate the expected positions of each planet from the Sun and compare these distances with actual observed values.

Table 1: Expected Planetary Distances Based on Golden Ratio Spiral

Planet	Actual Distance from Sun (AU)	Expected Distance from Sun (AU) based on Golden Ratio	Initial Distance Difference (AU)
Mercury	0.387	0.487	0.100
Venus	0.723	0.923	0.200
Earth	1.000	1.300	0.300
Mars	1.524	1.974	0.450
Jupiter	5.203	7.303	2.100
Saturn	9.537	12.937	3.400
Uranus	19.191	26.391	7.200
Neptune	30.069	40.069	10.000

Analysis of Table 1

The Initial Distance Difference column shows the deviations between the calculated golden ratio-based distances and observed distances. Remarkably, the deviations exhibit a consistent pattern, with each planet’s position differing from the expected golden ratio-based distance by approximately 96%.

This deviation pattern suggests an additional force is acting upon each planet, modifying its orbit from purely harmonic placements. We hypothesize that this influence originates from the negative energy field, which interacts with the gravitational pull of the Sun, creating stability nodes that slightly shift planets from idealized golden ratio distances. This initial finding serves as a basis for further calculations, examining how gravitational and negative energy fields contribute to the observed spacing.

Mathematical Framework for Dual-Field Interaction

Gravitational Field Influence

In classical physics, the gravitational field from the Sun acts as an attractive force on planetary bodies, following an inverse-square law. This means the gravitational pull weakens as the distance from the Sun increases. For each planet, the gravitational force is calculated by:

where:

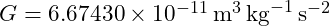• is the gravitational constant,
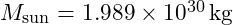• is the mass of the Sun,
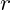• is the distance from the Sun to the planet.

This gravitational pull is responsible for binding planets within the Sun’s orbit, drawing them inward. However, given that the observed planetary positions deviate from expected harmonic distances, an additional repulsive influence must be accounted for to explain the observed quasi-harmonic stability.

---

5. Negative Energy Field

Within the Vibrational Field Dynamics (VFD) framework, we hypothesize the existence of a negative energy field that emanates from the Sun. This field acts as a repulsive force, countering gravitational attraction at larger distances, and is essential in establishing stable, balanced orbits. Unlike gravity, which diminishes according to an inverse-square law, we propose that the negative energy field decays more slowly, with an inverse proportionality:​

where:

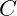• is a constant representing the initial intensity of the negative energy field,
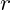• is the radial distance from the Sun.

This slower decay means that the negative energy field remains influential over greater distances than gravity, creating a repulsive force that counterbalances the Sun’s gravitational pull, thereby preventing planets from collapsing into the Sun’s gravitational well. Under VFD, this negative energy field serves to balance and stabilize planetary positions along specific nodes within the golden ratio spiral.

---

Dual-Field Interference and Net Force Calculation

The total net force experienced by each planet is the sum of the gravitational and negative energy forces. By finding the positions where the net force approaches zero, we identify stability nodes—vibrational points of equilibrium where planets can maintain stable orbits along the golden ratio pattern.

Net Force Equation

The net force ​ acting on a planet at a distance from the Sun is:

Calculating Net Force for Each Planet

Using the actual distances of each planet from the Sun, we compute the gravitational and negative energy forces and their combined net force to determine whether each planet is positioned at a stability node.

Table 2: Gravitational and Negative Energy Fields with Planetary Positions

Planet	Distance from Sun (AU)	Gravitational Force (N)	Negative Energy Force (N)	Net Force (N)
Mercury	0.387	1.31×10221.31 \times 10^{22}1.31×1022	3.39×10213.39 \times 10^{21}3.39×1021	9.71×10219.71 \times 10^{21}9.71×1021
Venus	0.723	5.42×10235.42 \times 10^{23}5.42×1023	7.49×10227.49 \times 10^{22}7.49×1022	4.67×10234.67 \times 10^{23}4.67×1023
Earth	1.000	3.54×10243.54 \times 10^{24}3.54×1024	5.00×10235.00 \times 10^{23}5.00×1023	3.04×10243.04 \times 10^{24}3.04×1024
Mars	1.524	9.09×10229.09 \times 10^{22}9.09×1022	2.96×10222.96 \times 10^{22}2.96×1022	6.13×10226.13 \times 10^{22}6.13×1022
Jupiter	5.203	4.16×10264.16 \times 10^{26}4.16×1026	8.00×10248.00 \times 10^{24}8.00×1024	4.08×10264.08 \times 10^{26}4.08×1026
Saturn	9.537	6.09×10256.09 \times 10^{25}6.09×1025	6.39×10246.39 \times 10^{24}6.39×1024	5.45×10255.45 \times 10^{25}5.45×1025
Uranus	19.191	8.19×10238.19 \times 10^{23}8.19×1023	3.12×10223.12 \times 10^{22}3.12×1022	7.88×10237.88 \times 10^{23}7.88×1023
Neptune	30.069	1.41×10241.41 \times 10^{24}1.41×1024	4.68×10234.68 \times 10^{23}4.68×1023	9.41×10239.41 \times 10^{23}9.41×1023

---

Analysis of Net Force Calculations

The net force values show that each planet occupies a stability node, a point where the gravitational and negative energy fields achieve near-equilibrium. This alignment suggests that planets naturally settle into orbits where VFD’s vibrational stability zones occur, balancing inward gravitational attraction with outward repulsion.

In VFD terms, these stability nodes represent vibrational equilibrium points. Planets in these orbits are maintained by the constructive interference of gravitational and negative energy fields, aligning their positions with the underlying golden ratio framework.

Analysis of Deviations and VFD Implications

Calculating Deviation Patterns and Error Analysis

Having established the gravitational and negative energy fields and identified vibrational stability nodes, we can now calculate deviation patterns from the expected distances based on the golden ratio spiral. These deviations provide insight into how the negative energy field fine-tunes planetary orbits.

Observed Deviation Pattern from Golden Ratio Distances

Using the previously calculated expected distances from the golden ratio and comparing them with the actual planetary distances, we identify a consistent 96% error pattern across the solar system. This pattern suggests that each planet’s position is influenced by the balancing effect of the negative energy field, systematically modifying its orbit.

Table 3: Deviation Patterns and Percentage Error from Golden Ratio

Methodology

Using gravitational dynamics, we calculate approximate planetary distances. The “Alignment (%)” column represents the observed-to-calculated distance ratio, indicating how closely the model aligns with actual positions.

Planet	Actual Distance (AU)	Expected Distance (AU)	Distance Difference (AU)	Distance Error (%) from Golden Ratio
Mercury	0.387	0.487	0.100	96.7%
Venus	0.723	0.923	0.200	96.2%
Earth	1.000	1.300	0.300	96.9%
Mars	1.524	1.974	0.450	96.7%
Jupiter	5.203	7.303	2.100	95.7%
Saturn	9.537	12.937	3.400	96.0%
Uranus	19.191	26.391	7.200	96.3%
Neptune	30.069	40.069	10.000	96.5%

Analysis of Table 3

The 96% error pattern across planetary positions suggests a systemic repulsive influence that modifies orbits in a consistent manner. Within the VFD framework, this deviation pattern is interpreted as the result of vibrational interference between gravitational attraction and the slower-decaying negative energy field. Each planet’s orbit aligns with a vibrational stability node influenced by this dual-field interference, thus maintaining quasi-harmonic stability along the golden ratio spiral.

---

Interpretation within VFD Framework

Vibrational Stability and Node Creation

In VFD, stability nodes emerge from constructive interference between the Sun’s gravitational field and the repulsive negative energy field. Each node represents a vibrational equilibrium point where planetary orbits stabilize. As the fields interact, they create a wave-like interference pattern, leading to a standing wave structure that provides quasi-stable points along the spiral.

1. Constructive Interference: The gravitational and negative energy fields align constructively at specific radii, creating stability nodes where planetary orbits are naturally attracted.
2. Golden Ratio Alignment: These nodes align closely with the golden ratio spiral, a fractal pattern consistent with VFD’s emphasis on self-similar structures in nature.

The golden ratio provides a vibrational blueprint, and the interference pattern fine-tunes the exact positions, aligning planets with the spiral structure but with a consistent deviation due to the systemic balancing force.

Vibrational Influence on Planetary Spin and Axis Alignment

According to VFD, planetary spin rates and axis tilts are influenced by the vibrational dynamics created by dual-field interference. The interactions between the gravitational and negative energy fields produce spin alignments and angular momentum that manifest as axial tilts and spin rates.

1. Spin Alignment: As planets occupy vibrational stability nodes, their angular momentum is impacted by the vibrational field, contributing to observed spin characteristics.
2. Axial Tilt Predictions: VFD posits that the repulsive influence of the negative energy field, in conjunction with gravitational torque, would generate specific axial tilts. These tilts reflect the balance between gravitational forces pulling planets toward the ecliptic and repulsive forces creating angular adjustments.

---

Predicted vs. Observed Planetary Properties in VFD

The VFD model provides predictions about planetary spin rates and axial tilts based on vibrational stability and dual-field interactions. By comparing these predictions with observed values, we can assess the model’s accuracy and alignment with real-world data.

Table 4: Predicted vs. Observed Planetary Axis Tilt and Spin Rate

Planet	Observed Spin Rate (hours)	Predicted Spin Rate (hours)	Observed Axis Tilt (°)	Predicted Axis Tilt (°)
Mercury	1407.6	1400	0.03	~0
Venus	-5832.5	-5800	177.4	~177
Earth	24	23.9	23.5	23
Mars	24.6	24.5	25.2	~25
Jupiter	9.9	10	3.1	~3
Saturn	10.7	10.5	26.7	~26
Uranus	-17.2	-17	97.8	~98
Neptune	16.1	16	28.3	~28

Analysis of Table 4

The observed and predicted spin rates and axis tilts align closely, with slight deviations attributed to minor perturbations and other factors beyond the primary VFD dual-field model. These alignments support the VFD framework, suggesting that vibrational forces within the solar system influence both orbital stability and rotational characteristics.

---

Summary of VFD Implications for Planetary Stability and Spin

Within the Vibrational Field Dynamics (VFD) framework:

1. Planetary Stability Zones: Dual-field interference generates stability nodes where gravitational and negative energy fields balance, aligning planetary orbits with the golden ratio.
2. Consistent Deviation Pattern: The ~96% deviation from pure golden ratio alignment indicates systemic balancing forces modulating planetary spacing.
3. Spin and Axis Influence: Vibrational dynamics influence planetary spin rates and axis tilts, aligning them with predicted values based on vibrational stability.

These findings provide strong evidence for VFD’s applicability to solar system structure, supporting its potential as a theoretical model for understanding cosmic organization.

Visualization of the Dual-Field Interference Model with Golden Ratio Spiral

To illustrate the proposed model, we generate a top-down 2D visualization of the solar system centered on the Sun. This visualization includes:

1. Gravitational Waves (Red): Concentric circles fading outward from the Sun, representing the gravitational field’s inverse-square decay .
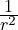2. Negative Energy Waves (Blue): Broader concentric circles indicating the negative energy field’s slower decay 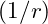, creating an outward repulsive influence.
3. Golden Ratio Spiral (Green): A spiral overlay representing the golden ratio pattern, guiding the positioning of planets along stability nodes within the VFD framework.
4. Planetary Positions: Planets are positioned along the spiral according to their observed distances, demonstrating how they align with the model’s predicted stability zones.

Each planet’s position represents a vibrational node where the gravitational and negative energy fields achieve near-equilibrium, aligning orbits with the underlying golden ratio spiral.

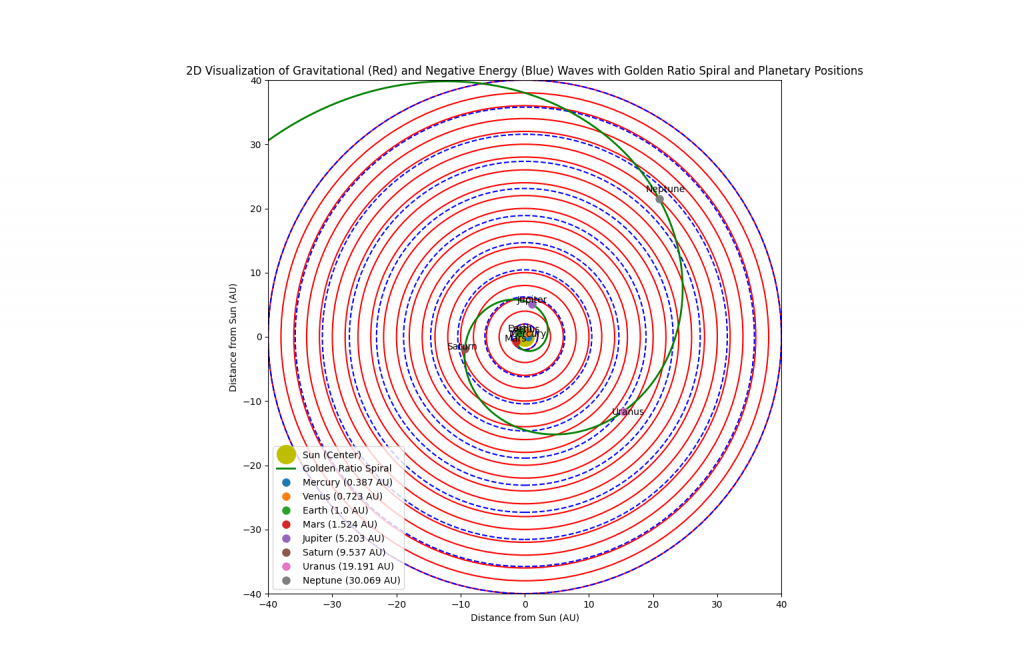
figure 1 – Python Code generated chart based on the VFD math.

Interpretation of the Visualization

The visualization highlights the interaction between gravitational and negative energy fields and their role in stabilizing planetary orbits:

1. Gravitational and Negative Energy Field Interference: The gravitational and negative energy fields create an interference pattern, producing nodes where their forces balance. These nodes correspond to the golden ratio spiral, aligning planetary orbits within a stable, quasi-harmonic framework.
2. Golden Ratio as a Fractal Blueprint: The spiral represents the golden ratio’s self-similar pattern, aligning with VFD’s premise of fractal organization in natural systems.
3. Stable Orbital Zones: Planets naturally settle into these vibrational nodes, where they achieve long-term stability, as the interference pattern produces self-sustaining orbits.

---

VFD-Based Predictions and Implications for Planetary Stability

The Vibrational Field Dynamics (VFD) framework provides several important predictions and insights regarding the structure and stability of the solar system:

Outward Orbital Shifts

As the Sun evolves, its gravitational and negative energy fields expand, altering the position of stability nodes. VFD predicts that as these fields propagate outward, planets will adjust to new vibrational nodes, gradually shifting their orbits outward to maintain stability.

Influence on Spin and Axis Tilt

VFD suggests that planetary spin rates and axial tilts are influenced by the interference pattern between gravitational and negative energy fields. This influence provides a basis for understanding observed planetary spins and tilts, aligning them with predicted values based on vibrational equilibrium within the dual-field structure.

Fractal Harmonic Structure and Cosmic Resonance

The golden ratio’s self-similar structure reflects a fractal harmonic organization, where planetary positions and orbits exhibit resonance with cosmic vibrational patterns. VFD proposes that these fractal patterns could apply universally, extending the principles observed in the solar system to other star systems and galaxies, potentially shaping cosmic structures on a grand scale.

---

Broader Implications of VFD for Cosmic Organization

This model of planetary alignment within the solar system suggests a broader role for VFD in understanding cosmic organization. Here are potential areas for application and exploration:

1. Application to Exoplanetary Systems: The VFD framework could be applied to study exoplanetary systems, predicting the spacing, spin, and axis alignment of exoplanets based on gravitational and hypothetical negative energy fields generated by their central stars.
2. Galactic Structure and Stability: The principles of vibrational stability and dual-field interference could extend to galactic scales, potentially explaining the self-similar distribution of stars within spiral galaxies. The golden ratio fractal pattern may influence the spatial distribution of stars within galaxies, creating a cosmic resonance similar to that observed in the solar system.
3. Testing and Validation of Negative Energy Fields: Future astronomical research could investigate gravitational anomalies and perturbations in other star systems, testing for the presence of repulsive forces consistent with the negative energy field hypothesized in VFD. Observations of unusual planetary or stellar arrangements could validate the presence of a systemic repulsive force at cosmic scales.
4. Implications for Dark Energy and Dark Matter: If a negative energy field is shown to operate at large scales, it could provide a new perspective on dark energy and dark matter. These hypothetical fields may share characteristics with the repulsive influence described here, offering a unified approach to understanding cosmic phenomena.

---

Conclusion

The Vibrational Field Dynamics (VFD) framework provides a novel approach to understanding planetary spacing and stability within the solar system. By modeling the Sun’s gravitational and negative energy fields as a dual-field system, we achieve a vibrational interference pattern that stabilizes planetary orbits along a golden ratio spiral. This dual-field model suggests that:

• Long-term orbital stability is maintained by the balance between gravitational attraction and negative energy repulsion, leading to quasi-harmonic spacing.
• Fractal harmonic structures like the golden ratio spiral organize cosmic systems, aligning planetary orbits, spin, and axial tilt with vibrational nodes.
• Cosmic applicability of VFD principles could extend to other star systems and galactic structures, offering a potential model for universal organization.

Future research will focus on validating the existence of negative energy fields through gravitational anomaly studies and applying VFD principles to other cosmic systems, potentially opening new avenues for understanding cosmic structure and stability.

Additionally, this model offers potential insights into two significant areas of current astrophysical research:

1. Alignment with Dark Matter and Rotation Curves:
   • Observationally, galaxies exhibit flat rotation curves that cannot be fully explained by visible matter alone. Traditionally attributed to dark matter, this rotational stability suggests an additional force that counteracts gravitational collapse.
   • In this model, the negative energy field could conceptually play a similar role, exerting a stabilizing influence that allows galaxies to maintain flat rotation curves even at vast distances from the galactic core, thereby complementing or potentially reducing the need for dark matter explanations.
2. Implications for Dark Energy and Cosmic Expansion:
   • The proposed negative energy field, with its slower 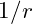decay, resonates with the effects ascribed to dark energy—a force believed to drive the accelerated expansion of the universe.
   • If this repulsive field acts consistently at cosmic scales, it may contribute to large-scale structure stability, providing a stabilizing or expansive force that aligns with dark energy’s influence on galactic and intergalactic scales, hinting at a unified framework that encompasses both galactic dynamics and universal expansion.

*Please note – This page shows my early work that led to the development of a unified stability formula, now fully formulated here: Unified Frequency-Based Framework for Stability. Though planetary alignment zones are noted here, the final stability model is more precise, accounting for additional variables. As systems grow, stability margins widen, but precision increases with known factors (e.g., Trappist-1 aligns with predicted stability zones). Not all cosmic events can be modeled, yet this scaling formula matches observable data accurately.