The Math of a Unified Theory of Vibrational Field Dynamics

1. Wave Equation for Vibrational Field Dynamics

In Vibrational Field Dynamics (VFD), the universe emerges from a fundamental vibrational field that governs the propagation of energy, matter, and forces. The wave equation is central to this theory, describing how vibrational disturbances propagate through the medium of the vibrational field, leading to the emergence of particles, forces, and cosmic structures.

The wave equation governing the vibrational field can be written as:

$(\partial_\mu \partial^\mu + m^2)\Phi + \xi R \Phi + \lambda \Phi^3 = 0$

Where:

Where:
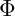$\Phi$ is the vibrational potential at any point in space and time.
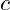$c$ is the speed of wave propagation within the vibrational field.
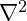$\nabla^2$ is the Laplacian operator.
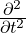$\frac{\partial^2}{\partial t^2}$ describes the time evolution of the vibration.

This equation serves as the foundation for modeling how vibrational waves in the unified field give rise to particles and forces, as well as cosmic structures such as stars and galaxies.

2. Harmonic Oscillators and Quantized Vibrations in the Vibrational Field

In Unified Vibrational Field Theory (UVFT), all matter and forces emerge from specific vibrational frequencies of the field. Quantized vibrational modes in this field correspond to fundamental particles such as electrons, protons, and photons. These particles are described as standing wave patterns within the vibrational field.

The harmonic oscillator model is employed to represent these quantized vibrations. The total energy of the system is given by the Hamiltonian equation:

$H = \frac{p^2}{2m} + \frac{1}{2} m \omega^2 x^2$

Where:

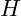$H$ is the Hamiltonian, or total energy of the vibrating system.
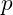$p$ represents the momentum of the particle or vibration.
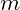$m$ is the mass equivalent (inertia) of the vibrating structure.
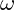$\omega$ is the angular frequency of the vibration.
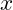$x$ is the position or displacement from equilibrium.

The quantized energy levels for this oscillator are given by:

$E_n = \hbar \omega \left( n + \frac{1}{2} \right)$

Where:

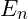$E_n$ denotes the energy of the quantized vibrational mode.
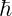$\hbar$ is the reduced Planck constant, defining the smallest unit of energy.
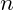$n$ is a non-negative integer, representing the quantum state of the vibration.

In this context, UVFD proposes that particles arise from distinct quantized vibrational modes, with their properties determined by the frequency and amplitude of the underlying vibrations.

3. Maxwell’s Equations within Vibrational Field Dynamics

To incorporate electromagnetic phenomena within Vibrational Field Dynamics, Maxwell’s equations must be adapted to describe how electromagnetic fields arise from vibrations in the unified field. These equations express how the vibrational energy of the field creates electromagnetic forces.

Gauss’s Law for Electricity:

$\nabla \cdot \mathbf{E} = \frac{\rho}{\varepsilon_0}$

Where:

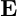$\mathbf{E}$ is the electric field.
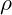$\rho$ is the charge density.
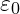$\varepsilon_0$ is the permittivity of free space, representing how the vibrational field supports electric field propagation.

Gauss’s Law for Magnetism:

$\nabla \cdot \mathbf{B} = 0$

Where:

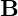$\mathbf{B}$ is the magnetic field, implying that magnetic monopoles do not exist in this framework, and the magnetic field lines form closed loops.

Faraday’s Law of Induction:

$\nabla \times \mathbf{E} = - \frac{\partial \mathbf{B}}{\partial t}$

This equation describes how changing magnetic fields induce electric fields. In UVFT, this represents vibrational interactions within the unified field that generate electromagnetic waves.

Ampère’s Law (with Maxwell’s Correction):

$\nabla \times \mathbf{B} = \mu_0 \mathbf{J} + \mu_0 \varepsilon_0 \frac{\partial \mathbf{E}}{\partial t}$

Where:

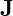$\mathbf{J}$ is the current density.
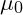$\mu_0$ is the permeability of free space, which in UVFT reflects the field’s resistance to magnetic vibrations.

These equations in UVFT describe how electromagnetic waves (such as light) propagate through the vibrational field, with the permittivity and permeability of the field dictating the speed of light.

4. Planck’s Constant and Etheric Vibrations

In Vibrational Field Dynamics, Planck’s constant $h$ plays a critical role in defining the smallest unit of vibrational energy within the unified field. The relationship between energy and frequency in this model follows the quantum mechanical principle:

$E = h f$

Where:

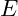$E$ represents the energy of the vibrational mode.
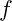$f$ is the frequency of the vibration.
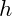$h$ is Planck’s constant, which defines the quantization of etheric vibrations.

This equation indicates that higher-frequency vibrations within the unified field correspond to higher-energy particles, while lower-frequency vibrations correspond to lower-energy particles. This relationship is crucial to understanding the quantum nature of particles as manifestations of vibrational patterns in the unified field.

5. Harmonic Patterns in Vibrational Field Dynamics

Unified Vibrational Field Theory integrates principles of sacred geometry and harmonic patterns to explain how vibrations organize into stable structures like particles and cosmic phenomena. The stability of these structures is rooted in harmonic relationships, such as the golden ratio ( $Phi$ ) and the Fibonacci sequence, which appear in nature and geometry.

Golden Ratio and Fibonacci Sequence:

$\Phi = \frac{1 + \sqrt{5}}{2} \approx 1.618$

The golden ratio manifests in naturally occurring patterns, such as the spirals in galaxies, DNA, and plant growth. In UVFT, vibrational modes that align with the golden ratio are considered to be in resonant states of high stability, allowing them to form stable structures like particles, atoms, and biological systems.

6. Non-Linear Dynamics and Chaos in the Vibrational Field

The unified vibrational field can exhibit non-linear behavior, where interactions between multiple waves create complex, chaotic systems. This non-linearity can give rise to organized structures such as planets, stars, and living organisms, similar to how chaos theory describes self-organizing systems in nature.

The Lorenz Equations are often used to describe chaotic systems, and they could be adapted to represent interactions within the vibrational field:

$\frac{dx}{dt} = \sigma (y - x)$

$\frac{dy}{dt} = x (\rho - z) - y$

$\frac{dz}{dt} = xy - \beta z$

Where:

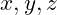$x, y, z$ represent variables describing the system’s state.
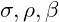$\sigma, \rho, \beta$ are parameters that govern the system’s behavior.

In UVFT, these equations may represent the non-linear interactions of vibrational waves in the field, ultimately giving rise to the self-organizing structures we observe in the universe.

7. General Relativity and the Vibrational Field as a Gravitational Medium

In Unified Vibrational Field Theory, gravity is interpreted not just as the curvature of spacetime, but as a result of distortions in the vibrational field caused by massive objects. Einstein’s field equations can be modified to incorporate the vibrational density of the field as the underlying cause of gravitational effects:

$R_{\mu\nu} - \frac{1}{2} g_{\mu\nu} R = \frac{8 \pi G}{c^4} T_{\mu\nu} + \Lambda g_{\mu\nu}$

Where:

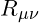$R_{\mu\nu}$ is the Ricci curvature tensor.
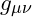$g_{\mu\nu}$ is the metric tensor, describing the geometry of spacetime.
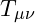$T_{\mu\nu}$ is the stress-energy tensor, representing matter and energy.
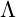$\Lambda$ is the cosmological constant, which in UVFT represents the energy density of the unified vibrational field..

In this model, the curvature of spacetime is seen as a reflection of the vibrational density of the field, where massive objects compress the field and generate gravitational effects.

The Math of a Unified Theory of Vibrational Field Dynamics

1. Wave Equation for Vibrational Field Dynamics

2. Harmonic Oscillators and Quantized Vibrations in the Vibrational Field

3. Maxwell’s Equations within Vibrational Field Dynamics

Gauss’s Law for Electricity:

Gauss’s Law for Magnetism:

Faraday’s Law of Induction:

Ampère’s Law (with Maxwell’s Correction):

4. Planck’s Constant and Etheric Vibrations

5. Harmonic Patterns in Vibrational Field Dynamics

Golden Ratio and Fibonacci Sequence:

6. Non-Linear Dynamics and Chaos in the Vibrational Field

7. General Relativity and the Vibrational Field as a Gravitational Medium

Leave a Reply Cancel reply

About Cookies